9 Contoh soal dinamika rotasi dan pembahasan

Contoh soal dinamika rotasi nomor 1

Batang AD ringan panjangnya 1,5 m. Batang bisa berputar di titik C dan diberi tiga gaya seperti gambar.

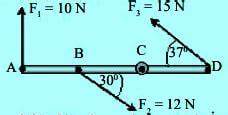
AB = 0,5 m dan CD = 0,5 m. Torsi yang bekerja pada batang terhadap titik C adalah …
A. 17,5 Nm berputar searah jarum jam
B. 17,5 Nm berputar berlawanan jarum jam
C. 2,5 Nm berputar searah jarum jam
D. 2,5 Nm berputar berlawanan jarum jam
E. 3,5 Nm berputar searah jarum jam

Pembahasan

τ = F₁ . L₁ – F₂ . L₂ – F₃ . L₃
τ = 10 N . 1 m – 12 N . 0,5 m sin 30^o – 15 N . 0,5 m . sin 37^o
τ = 10 Nm – 3 Nm – 4,5 Nm = 2,5 Nm

Soal ini jawabannya C.

Contoh soal dinamika rotasi nomor 2

Bola pejal bermassa 2,5 kg dan jari-jari 0,12 m menggelinding pada lantai mendatar bersamaan cincin yang bermassa 1 kg dan jari-jari 0,12 m. Perbandingan momen inersia bola pejal dan cincin sebesar …
A. 5 : 2
B. 2 : 1
C. 1 : 1
D. 2 : 5
E. 1 : 2

Pembahasan

Momen inersia bola pejal sebagai berikut.

I = 2/5 MR²
I = 2/5 . 2,5 kg . (0,12 m)²
I = 0,0144 kgm²

Momen inersia cincin atau silinder berongga sebagai berikut.

I = MR²
I = 2,5 kg . (0,12 m)²
I = 0,036 kgm²

Jadi perbandingan momen inersia bola pejal dan cincin = 0,0144 : 0,036 = 2 : 5. Soal ini jawabannya D.

Contoh soal dinamika rotasi nomor 3

Sebuah roda pejal jari-jarinya 20 cm dan massanya 5 kg. Pada roda itu bekerja momen gaya sebesar 10 Nm. Besar percepatan sudut roda itu adalah …
A. 0,1 rad/s²
B. 5 rad/s²
C. 10 rad/s²
D. 20 rad/s²
E. 100 rad/s²

Pembahasan

τ = I . α
τ = 1/2 MR² . α
10 Nm = 1/2 . 5 kg . (0,2 m)² . α
10 Nm = 0,1 kgm² . α
α = 10 Nm / 0,1 kgm² = 100 rad/s²

Soal ini jawabannya E.

Contoh soal dinamika rotasi nomor 4

Sebuah yoyo dililit tali cukup panjang dan ditarik oleh gaya F = 10 N seperti pada gambar.

Massa yoyo 2,5 kg dan jari-jari = 10 cm. Percepatan linear pusat massa yoyo adalah …
A. 10 m/s²
B. 7,5 m/s²
C. 5,0 m/s²
D. 4,0 m/s²
E. 2,5 m/s²

Pembahasan

Hitung terlebih dahulu percepatan sudut yoyo dengan cara dibawah ini.

τ = I . α
F . 1/2R + fg . R = 1/2 . MR² . α
10 N . 1/2R + fg . R = 1/2 . 2,5 kg . (R)² . a/R
5 + fg = 1,25 a … (pers. 1)

Dari hukum Newton diperoleh.

F – fg = m a
10 – fg = 2,5 a … (pers. 2)

Eliminasi persamaan 1 dan 2.

5 + fg = 1,25 a
10 – fg = 2,5 a
__________________+
15 = 3,75a
a = 15/3,75 = 4 m/s²

Soal ini jawabannya D.

Contoh soal dinamika rotasi nomor 5

Benda A bermassa m diikat dengan tali yang panjangnya 1 m. Benda B memiliki massa 3m diikat dengan tali dengan panjang sama dengan benda A. Bila A dan B diputar dengan kecepatan sudut sama maka besar momentum sudut B …
A. 3 kali momentum sudut A
B. 1/3 kali momentum sudut A
C. 9 kali momentum sudut A
D. 1/9 kali momentum sudut A
E. √ 3 kali momentum sudut A

Pembahasan

Momentum sudut benda A sebagai berikut.

L_A = I . ω
L_A = m . r² . ω
L_A = m . (1 m)² . ω
L_A = mω

Momentum sudut benda B sebagai berikut.

L_B = I . ω
L_B = m . r² . ω
L_A = 3m . (1 m)² . ω
L_A = 3mω

Jadi perbandingan momentum sudut benda A dan benda B = L_A : L_B = mω : 3 mω = 1 : 3. Dengan kata lain momentum sudut benda B = 3 kali momentum sudut benda A. Soal ini jawabannya A.

Contoh soal dinamika rotasi nomor 6

Seorang penari balet berputar dengan dengan kecepatan sudut ω memiliki momen inersia sebesar I. Agar penari tersebut bergerak dengan kecepatan sudut yang lebih besar yang harus dilakukan penari tersebut adalah …
A. meregangkan lengannya agar momen inersianya lebih besar
B. menekuk kedua lengannya agar momen inersianya lebih besar
C. meregangkan kedua lengannya agar momen inersianya menjadi lebih kecil
D. menekuk kedua lengannya agar momen inersianya menjadi lebih kecil
E. menekuk kedua kakinya agar lebih pendek

Pembahasannya.

Yang harus dilakukan oleh penari agar kecepatan sudut lebih besar adalah menekuk kedua lengannya sehingga momen inersiannya menjadi lebih kecil. Soal ini jawabannya D.

Contoh soal dinamika rotasi nomor 7

Seorang anak laki-laki berdiri diatas papan yang dapat berputar bebas. Saat kedua lengannya terentang, kecepatan sudutnya 0,25 putaran/detik. Tetapi saat kedua lengan tertekuk kecepatannya menjadi 0,8 putaran/detik, maka perbandingan momen inersia anak waktu kedua tangan terentang dengan sesudah menekuk adalah …
A. 3 : 1
B. 1 : 3
C. 1 : 2
D. 5 : 16
E. 16 : 5

Pembahasan

I₁ . ω₁ = I₂ . ω₂
I₁ . 0,25 putaran/detik = I₂ . 0,8 putaran/detik
I₁ : I₂ = 0,25 : 0,8 = 5 : 16

Soal ini jawabannya D.

Contoh soal dinamika rotasi nomor 8

Silinder pejal dan roda yang memiliki massa dan jari-jari sama masing-masing 4 kg dan 50 cm. Kedua benda menggelinding dengan kecepatan yang sama pula yaitu 5 m/s. Perbandingan energi kinetik silinder dan roda adalah …
A. 3 : 4
B. 4 : 3
C. 3 : 2
D. 2 : 3
E. 14 : 15

Pembahasan

Energik kinetik rotasi silinder pejal sebagai berikut.