Postingan ini membahas contoh soal fungsi injektif, fungsi surjektif, fungsi bijektif, fungsi onto dan pembahasannya. Fungsi injektif atau fungsi satu-satu adalah fungsi yang memasangkan anggota domain sedemikian sehingga setiap anggota domain mempunyai pasangan yang berbeda. Fungsi f : A → B, adalah fungsi injektif apabila f(a) = f(b) maka a = b.
Fungsi surjektif atau fungsi onto adalah fungsi yang memasangkan anggota domain sedemikian sehingga setiap anggota daerah kodomain mempunyai pasangan dengan anggota domain. Fungsi f : A → B, adalah fungsi surjektif apabila setiap b ∈ B merupakan peta dari a ∈ A.
Fungsi bijektif adalah fungsi injektif sekaligus fungsi surjektif. Fungsi f : A → B adalah fungsi bijektif apabila setiap b ∈ B merupakan peta dari a ∈ A, dan jika f(a) = f(c) maka a = c. Perbedaan antara fungsi injektif, fungsi surjektif dan fungsi bijektif dapat dilihat pada gambar dibawah ini.

Contoh soal 1
Dari fungsi-fungsi yang disajikan dalam diagram panah berikut, manakah yang merupakan fungsi injektif, fungsi surjektif atau fungsi bijektif ?.

Pembahasan / penyelesaian soal
- Gambar (a) adalah fungsi injektif karena anggota domain mempunyai pasangan yang berbeda di kodomain.
- Gambar (b) adalah fungsi surjektif karena semua anggota kodomain mempunyai pasangan di domain.
- Gambar (c) adalah fungsi bijektif karena fungsi injektif sekaligus fungsi surjektif.
- Gambar (d) adalah fungsi bijektif karena fungsi injektif sekaligus fungsi surjektif.
- Gambar (e) adalah fungsi surjektif karena anggota kodomain mempunyai pasangan di anggota domain.
Contoh soal 2
Diketahui fungsi A = {1, 2, 3, 4} dan B = {5, 6, 7} yang dinyatakan dalam pasangan berurutan berikut ini, manakah yang merupakan pasangan surjektif ?.
- f = { (1, 6) ; (2, 6) ; (3, 6) ; (4, 6) }
- f = { (1, 5) ; (2, 6) ; (3, 6) ; (4, 5) }
- f = { (1,6) ; (2, 7) ; (3, 5) ; (4, 5) }
- f = { (1, 5) ; (2, 6) ; (3, 7) ; (4, 7) }
Pembahasan / penyelesaian soal
Fungsi A sebagai domain dan fungsi B sebagai kodomain.
- Bukan fungsi surjektif karena tidak semua anggota B (5 dan 7) mempunyai pasangan di A.
- Bukan fungsi surjektif karena tidak semua anggota B (7) mempunyai pasangan di A.
- Fungsi surjektif karena semua anggota B mempunyai pasangan di A.
- Fungsi surjektif karena semua anggota B mempunyai pasangan di A.
Contoh soal 3
Misal A = himpunan bilangan prima yang kurang dari 10 dan B = himpunan bilangan asli yang kurang dari 10. Pasangan terurut dibawah ini yang merupakan fungsi injektif adalah …
A. { (2, 2) ; (3, 1) ; (5, 1) ; (7, 1) }
B. { (2, 1) ; (3, 2) ; (5, 1) ; (7, 2) }
C. { (2, 1) ; (3, 2) ; (5, 3) ; (7, 4) }
D. { (2, 2) ; (3, 3) ; (5, 5) ; (7, 5) }
E. {(2, 4) ; (3, 4) ; (5, 4) ; (7, 4) }
Pembahasan / penyelesaian soal
A = {2, 3, 5, 7} sebagai domain dan B = {1, 2, 3, 4, 5, 6, 7, 8, 9} sebagai kodomain. Fungsi injektif jika anggota A mempunyai pasangan yang berbeda di B. Jadi jawaban soal ini sebagai berikut:
A. bukan fungsi injektif karena anggota A (3, 5, 7) mempunyai pasangan yang sama di B yaitu (1).
B. bukan fungsi injektif karena anggota A mempunyai pasangan yang tidak berbeda (yaitu 1 dan 2) di B.
C. Fungsi injektif karena setiap anggota A mempunyai pasangan yang berbeda di B.
D. bukan fungsi injektif karena anggota A (5 dan 7) mempunyai pasangan yang sama yaitu 5
E. bukan fungsi injektif karena anggota A mempunyai pasangan yang sama yaitu 4
Jadi soal ini jawabannya C.
Contoh soal 4
Fungsi dibawah ini yang merupakan fungsi bijektif adalah …
A. f(x) = x2 + 2
B. f(x) = 2x + 1
C. f(x) = 1 –
D. f(x) = sin 2x
E. f(x) = log x2
Pembahasan / penyelesaian soal
Yang merupakan fungsi bijektif adalah f(x) = 2x + 1 karena anggota domain akan memiliki pasangan yang berbeda di kodomainnya. Ini bisa dibuktikan dengan cara subtitusi nilai x seperti tabel dibawah ini.
| x (domain) | f(x) = 2x + 1 (kodomain) |
|---|---|
| -2 | 2 . – 2 + 1 = -3 |
| -1 | 2 . -1 + 1 = 0 |
| 0 | 2 . 0 + 1 = 1 |
| 1 | 2 . 1 + 1 = 3 |
| 2 | 2 . 2 + 1 = 5 |
Kita perhatikan tabel diatas, setiap anggota x (domain) mempunyai pasangan yang berbeda di kodomain f(x) dan semua anggota f(x) mempunyai pasangan di x. Jadi soal ini jawabannya B.
Contoh soal 5
Misal A = {2, 3, 4} dan B = {4, 9, 16}. Jika f : A → B dengan f(x) = x2, maka f adalah fungsi …
A. injektif
B. surjektif
C. bijektif
D. A dan B benar
E. A, B dan C benar
Pembahasan / penyelesaian soal
Karena f(x) = x2 maka jika dipasangkan f = {(2, 4) ; (3, 9) ; (4, 16) }. Kita perhatikan setiap anggota A mempunyai pasangan yang berbeda di B. Dan semua anggota B mempunyai pasangan di A. Sehingga fungsi ini adalah fungsi injektif sekaligus fungsi surjektif atau disebut dengan fungsi bijektif. Jadi soal ini jawabannya C.
Contoh soal 6
Fungsi dibawah ini yang merupakan fungsi bijektif adalah …
A. y = 1/2 x + 5
B. y = x2 + 3
C. y =
D. y = sin x
E. y = cos x
Pembahasan / penyelesaian soal
Yang merupakan fungsi bijektif adalah 1/2x + 5. Alasan sama seperti soal nomor 4.
Contoh soal 7
Jika f : A → B, dengan A = {1, 2, 3, 4} ; B = {0, 1} dan fungsi f dinyatakan dengan diagram berikut, fungsi f adalah fungsi …
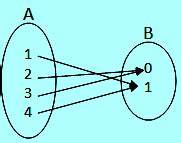
A. injektif
B. surjektif
C. bijektif
D. genap
E. ganjil
Pembahasan / penyelesaian soal
Fungsi pada gambar diatas adalah fungsi surjektif karena semua anggota B (0 dan 1) mempunyai pasangan di A. Jadi soal ini jawabannya B.
Contoh soal 8
Fungsi dibawah ini yang merupakan fungsi injektif adalah …
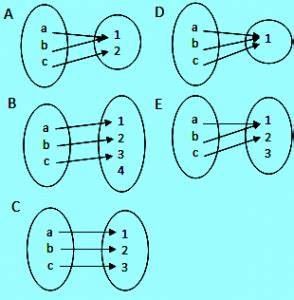
Pembahasan / penyelesaian soal
Yang merupakan fungsi injektif adalah B karena setiap anggota domain mempunyai pasangan yang berbeda di kodomainnya.