Artikel ini membahas contoh soal fungsi kuadrat dan pembahasannya + jawabannya. Lalu apa itu fungsi kuadrat ?. Suatu fungsi f pada himpunan bilangan real (R) yang ditentukan oleh f(x) = ax2 + bx + c dengan a, b, c ∈ R dan a ≠ 0 disebut fungsi kuadrat. Ada dua cara menggambar grafik fungsi kuadrat yaitu dengan menggunakan tabel koordinat bebarapa titik dan menggunakan titik-titik penting yang dilalui grafik. Titik-titik penting tersebut adalah titik potong grafik dengan sumbu X, titik potong grafik dengan sumbu Y dan titik balik.
Berdasarkan nilai diskriminannya (D = b2 – 4ac), grafik fungsi kuadrat (y = ax2 + bx + c) ) terdiri dari 6 kemungkinan yaitu sebagai berikut.
- Jika a > 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik yang berbeda. Jenis titik baliknya minimum.
- Jika a > 0 dan D = 0, grafik fungsi kuadrat memotong sumbu X di satu titik atau menyinggung sumbu X. Jenis titik baliknya minimum.
- Jika a > 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit positif). Jenis titik baliknya minimum.
- Jika a < 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik berbeda. Jenis titik baliknya maksimum.
- Jika a < 0 dan D = 0, grafik fungsi kuadrat menyinggung sumbu X dan titik baliknya maksimum.
- Jika a < 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit negatif) dan titik baliknya maksimum.
Contoh soal fungsi kuadrat kurikulum merdeka
Contoh soal fungsi kuadrat nomor 1
Tentukan koordinat titik puncak, sumbu simetri, koordinat titik potong dengan sumbu y, dan banyak titik potong dari grafik fungsi-fungsi kuadrat di bawah ini.
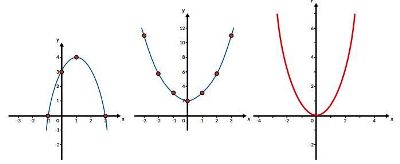
Apakah hubungan antara titik puncak dengan grafik terbuka ke atas atau ke bawah?
Pembahasan / penyelesaian soal
Gambar (1 = gambar paling kiri).
titik puncak = (1, 4)
sumbu simetri = x = 1
koordinat titik potong dengan sumbu y = (0, 3)
banyak titik potong = 2
Gambar (2 = gambar di tengah).
titik puncak = (0, 2)
sumbu simetri = x = 0
koordinat titik potong dengan sumbu y = (0, 2)
banyak titik potong = 0
Gambar (3 = gambar paling kanan).
titik puncak = (0, 0)
sumbu simetri = x = 0
koordinat titik potong dengan sumbu y = (0, 0)
banyak titik potong = 1
Hubungan antara titik puncak dengan grafik fungsi kuadrat terbuka ke atas atau ke bawah sebagai berikut.
Jika titik puncak menunjukkan nilai maksimum maka grafik fungsi kuadrat terbuka ke bawah. Contohnya gambar 1.
Jika titik puncak menunjukkan nilai minimum maka grafik fungsi kuadrat terbuka ke atas. Contohnya gambar 1 dan 2.
Contoh soal fungsi kuadrat nomor 2
Tentukan berapa banyak titik potong dari fungsi kuadrat berikut.
a. f(x) = 3x2 + 4x + 1
b. f(x) = – 4x2 + 4x + 5
c. f(x) = – 3x2 + 4x + 1
d. f(x) = 4x2 + 4x + 5
e. f(x) = x2 + 2x + 1
f. f(x) = – 2x2 + 3x + 5
g. f(x) = – 3x2 + 8x – 1
h. f(x) = 4x2 + 11x – 7
Pembahasan / penyelesaian soal
Jika D > 0 maka ada dua titik potong dengan sumbu x.
Jika D = 0 maka ada satu titik potong dengan sumbu x.
Jika D < 0 maka tidak ada titik potong dengan sumbu x.
Dengan menggunakan rumus D = b2 – 4ac maka diperoleh jawaban sebagai berikut.
a. D = 42 – 4 . 3 . 1 = 4 (D > 0 maka memiliki 2 titik potong)
b. D = 42 – 4 . (-4) . 5 = 96 (D > 0 maka memiliki 2 titik potong)
c. D = 42 – 4 . (-3) . 1 = 28 (D > 0 maka memiliki 2 titik potong)
d. D = 42 – 4 . 4 . 5 = – 64 (D < 0 maka tidak memiliki titik potong)
e. D = 22 – 4 . 1 . 1 = 0 (D = 0 maka memiliki satu titik potong)
f. D = 32 – 4 . (-2) . 5 = 49 (D > 0 maka memiliki 2 titik potong)
g. D = 82 – 4 . (-3) . (-1) = 52 (D > 0 maka memiliki 2 titik potong)
h. D = 112 – 4 . 4 . (-7) = 223 (D > 0 maka memiliki 2 titik potong)
Contoh soal fungsi kuadrat nomor 3
Fungsi kuadrat yang terbuka ke bawah adalah __________ (jawaban bisa lebih dari satu).
a. f(x) = x2 + 2x + 1
b. f(x) = -2x2 + 3x + 5
c. f(x) = -3x2 + 8x – 1
d. f(x) = 4x2 + 11x – 7
Pembahasan / penyelesaian soal
Fungsi kuadrat terbuka ke bawah jika a < 0.
a. f(x) = x2 + 2x + 1 (terbuka ke atas karena a > 0 (a = 1).
b. f(x) = -2x2 + 3x + 5 (terbuka ke bawah karena a < 0 (a = -2).
c. f(x) = -3x2 + 8x – 1 (terbuka ke bawah karena a < 0 (a = -3).
d. f(x) = 4x2 + 11x – 7 terbuka ke atas karena a > 0 (a = 4).
Jadi fungsi kuadrat yang terbuka ke bawah adalah b dan c.
Contoh soal fungsi kuadrat nomor 4
Fungsi kuadrat yang terbuka ke atas adalah ____________ (jawaban bisa lebih dari satu).
a. f(x) = 3x2 + 4x + 1
b. f(x) = -4x2 + 4x + 5
c. f(x) = -3x2 + 4x + 1
d. f(x) = 4x2 + 4x + 5
Pembahasan / penyelesaian soal
Fungsi kuadrat terbuka ke atas jika a > 0.
a. f(x) = 3x2 + 4x + 1 (terbuka ke atas karena a > 0 (a = 3).
b. f(x) = -4x2 + 4x + 5 (terbuka ke bawah karena a < 0 (a = -4)
c. f(x) = -3x2 + 4x + 1 (terbuka ke bawah karena a < 0 (a = -3)
d. f(x) = 4x2 + 4x + 5 (terbuka ke atas karena a > 0 (a = 4)
Jadi fungsi kuadrat yang terbuka ke atas adalah a dan d.
Contoh soal fungsi kuadrat nomor 5
Perhatikan tabel di bawah ini, yang menunjukkan jarak tempuh suatu mobil sebagai fungsi dari waktu.

a. Berapa jarak maksimum yang ditempuh?
b. Berapa koordinat titik maksimum?
c. Tentukan persamaan garis sumbu simetri?
Pembahsan / penyelesaian soal
a. Jarak maksimum = 17 m
b. Koordinat titik maksimum = (3, 17)
c. Persamaan sumbu simetri: x = 3
Contoh soal fungsi kuadrat nomor 6
Fungsi kuadrat untuk gerak bola adalah f(t) = -5t2 + 11t + 12.
a. Buatlah tabel dari t = 0 hingga t = 5 detik
b. Gambarkan grafiknya
c. Tentukan ketinggian maksimum
Pembahasan / penyelesaian soal
Subtitusi t = 0 hingga t = 5 ke f(t) = -5t2 + 11t + 12 dan diperoleh hasil sebagai berikut.
- (t = 0) maka f(0) = -5 . 02 + 11. 0 + 12 = 12
- (t = 1) maka f(1) = -5 . 12 + 11. 1 + 12 = 18
- (t = 2) maka f(2) = -5 . 22 + 11 . 2 + 12 = 14
- (t = 3) maka f(3) = -5 . 32 + 11 . 3 + 12 = 0
- (t = 4) maka f(4) = -5 . 42 + 11 . 4 + 12 = -24
- (t = 5) maka f(5) = -5 . 52 + 11 . 5 + 12 = -58
| t | 0 | 1 | 2 | 3 | 4 | 5 |
| f(t) | 12 | 18 | 14 | 0 | -24 | -58 |
Cara menggambar grafik fungsi kuadrat f(t) = -5t2 + 11t + 12 sebagai berikut.
- Tentukan titik potong sumbu x dengan cara memfaktorkan.
-5t2 + 11t + 12 = 0
(-5t – 4)(t – 3) = 0
t1 = 4/-5 = -0,8
t2 = 3
Titik potong sumbu x = (-0,8 ; 0) dan (3, 0).
- Tentukan titik potong sumbu y dengan cara subtitusi t = 0 ke f(t) = -5t2 + 11t + 12.
f(t) = -5t2 + 11t + 12
f(0) = -5 . 02 + 11 . 0 + 12 = 12)
Titik potong sumbu y = (0, 12)
- Tentukan koordinat titik puncak dengan cara di bawah ini.
→ xp = –
→ yp = –
→ yp = –
Koordinat titik puncak = (1,1 ; 18,05)
Jadi grafik f(t) = -5t2 + 11t + 12 sebagai berikut.

Berdasarkan grafik tersebut ketinggian maksimum = 18,05.
Contoh soal fungsi kuadrat nomor 7
Bola dilemparkan ke atas dari tanah dengan kecepatan tertentu sehingga ketinggian yang dicapai merupakan fungsi dari waktu, h(t) = -5t2 + 40t. Berapa ketinggian maksimum yang dicapai oleh bola.
Pembahasan / penyelesaian soal
Diketahui:
- h(t) = -5t2 + 40t
- a = -5
- b = 40
- c = 0
Ketinggian maksimum dihitung dengan rumus dibawah ini.
hmak = –hmak = –
hmak = –
Contoh soal fungsi kuadrat nomor 8
Pendapatan dari hasil penjualan barang P(q) ditentukan oleh jumlah barang yang diproduksi q. P(q) = -20q2 + 3.000q. Tentukan pendapatan maksimal atau optimal dan jumlah barang yang bersesuaian dengannya.
Pembahasan / penyelesaian soal
Diketahui:
- P(q) = -20q2 + 3.000q
- a = -20
- b = 3.000
- c = 0
Pendapatan maksimal dihitung dengan rumus dibawah ini.
Pmak = –Pmak = –
Pmak = –
Cara cari jumlah barang yang bersesuai dengan subtitusi P(q) = 112.500 ke P(q) = -20q2 + 3.000q.
- P(q) = -20q2 + 3.000q
- 112.500 = -20q2 + 3.000q (:20)
- 5.625 = -q2 + 150
- q2 – 150 + 5625 = 0
- (q – 75) (q – 75 ) = 0
- q = 75
Jumlah barang = 75.
Contoh soal Fungsi kuadrat pilihan ganda (PG)
Contoh soal fungsi kuadrat nomor 9
Persamaan sumbu simetri dari f(x) = 6 – 5x – x2 adalah …
A. x = -2
B. x = 2
C. x = -2
D. x = 3
E. x = 5
Pembahasan / penyelesaian soal
Diketahui:
- a = -1
- b = -5
- c = 6
Cara menjawab soal ini yaitu dengan menggunakan rumus persamaan sumbu simetri yaitu sebagai berikut.
→ Pers. sumbu simetri = –→ Pers. sumbu simetri = –
Soal ini jawabannya C.
Contoh soal fungsi kuadrat nomor 10
Grafik fungsi f(x) = x2 + 4x – 30 simetris terhadap garis x = a. Nilai a = …
A. -4
B. -2
C. -1
D. 2
E. 4
Pembahasan / penyelesaian soal
Dengan menggunakan rumus persamaan sumbu simetri diperoleh hasil sebagai berikut.
→ x = –→ a = –
Soal ini jawabannya B.
Contoh soal fungsi kuadrat nomor 11
Nilai m agar grafik fungsi y = (m – 1)x2 – 2mx + (m – 3) selalu berada dibawah sumbu X (definit negatif) adalah …
A. m = 1
B. m > 1
C. m < 1
D. m > 3/4
E. m < 3/4
Pembahasan / penyelesaian soal
Diketahui:
- a = m – 1
- b = -2m
- c = m – 3
Syarat definit negatif adalah a < 0 dan D < 0.
- a < 0
- m – 1 < 0
- m < 1
- D < 0
- b2 – 4ac < 0
- (-2m)2 – 4 (m – 1) (m – 3) < 0
- 4m2 – 4 (m2 – 4m + 3) < 0
- 4m2 – 4m2 + 16m – 12 < 0
- 16m – 12 < 0
- 16m < 12
- m <
- m < 3/4
Jadi nilai m < 3/4. Soal ini jawabannya E.
Contoh soal fungsi kuadrat nomor 12
Koordinat titik balik grafik y = x2 – 6x + 8 adalah …
A. (3, -1)
B. (-3, -1)
C. (4, 2)
D. (6, 8)
E. (-6, 8)
Pembahasan / penyelesaian soal
Diketahui:
- a = 1
- b = -6
- c = 8
Dengan menggunakan rumus koordinat titik balik diperoleh hasil sebagai berikut.
→ x = –→ x = –
→ y = –
→ y = –
→ y = –
→ y = –
Jadi koordinat titik balik (3, -1). Soal ini jawabannya A.
Contoh soal fungsi kuadrat nomor 13
Koordinat titik balik fungsi kuadrat f(x) = x2 – 2x – 3 adalah …
A. (1, 4)
B. (-1, 4)
C. (4, 1)
D. (1, -4)
E. (-1, -4)
Pembahasan / penyelesaian soal
→ x = –→ x = –
→ y = –
→ y = –
→ y = –
→ y = –
Jadi titik baliknya (1, -4). Soal ini jawabannya D.
Contoh soal fungsi kuadrat nomor 14
Perhatikan gambar fungsi kuadrat dibawah ini.

Persamaan fungsi kuadrat grafik diatas adalah…
A. y = x2 – 2x + 15
B. y = x2 – 2x – 15
C. y = x2 + 2x + 15
D. y = x2 – 8x – 15
E. y = x2 – 8x + 15
Pembahasan / penyelesaian soal
Berdasarkan grafik fungsi kuadrat diatas kita ketahui:
- x1 = -5
- x2 = -3
- y = 15
Fungsi kuadrat dibentuk dengan cara sebagai berikut:
- y = a (x – x1) (x – x2)
- y = a (x – (-5)) (x – (-3))
- y = a (x + 5) (x + 3)
- y = a (x2 + 3x + 5 x + 15)
- y = a (x2 + 8x + 15)
Selanjutnya kita tentukan nilai a dengan subtitusi nilai x = 0 dan y = 15 sehingga didapat:
- 15 = a (02 + 8 . 0 + 15)
- 15 = a . 15
- a = 15/15 = 1
Jadi fungsi kuadratnya adalah:
- y = 1 (x2 + 8x + 15)
- y = x2 + 8x + 15
Jadi soal ini jawabannya C.
Contoh soal fungsi kuadrat nomor 15

Persamaan fungsi kuadrat grafik diatas adalah…
A. y = 2x2 + 2x – 4
B. y = 2x2 – 2x – 4
C. y = x2 + x – 4
D. y = x2 – 2x – 4
E. y = x2 – x – 4
Pembahasan / penyelesaian soal
Berdasarkan grafik diatas kita ketahui:
- x1 = -1
- x2 = 2
- y = -4
Maka persamaan fungsi kuadrat sebagai berikut:
- y = a (x – (-1)) (x – 2)
- y = a (x + 1) (x – 2)
- y = a (x2 – x – 2)
Menentukan nilai a dengan cara subtitusi x = 0 dan y = -4 sehingga didapat hasil dibawah ini:
- -4 = a (02 – 0 – 2)
- -4 = a . -2
- a = -4/-2 = 2
Sehingga persamaan kuadratnya adalah:
- y = 2 (x2 – x – 2)
- y = 2x2 – 2x – 4
Soal ini jawabannya B.
Contoh soal fungsi kuadrat nomor 16
Perhatikan gambar dibawah ini.
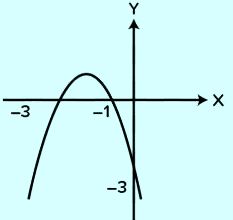
Jika fungsi kuadrat grafik diatas dinyatakan oleh f(x) = ax2 + bx + c maka pernyataan dibawah ini yang benar adalah…
A. a < 0, b < 0, dan c < 0
B. a < 0, b > 0 dan c > 0
C. a < 0, b > 0 dan c < 0
D. a > 0, b < 0 dan c > 0
E. a > 0, b < 0 dan c < 0
Pembahasan / penyelesaian soal
Untuk menjawab soal ini kita bentuk terlebih dahulu persamaan fungsi kuadrat grafik diatas sebagai berikut:
- y = a (x – (-3)) (x – (-1))
- y = a (x + 3) (x + 1)
- y = a (x2 + 4x + 3)
- -3 = a (02 + 4 . 0 + 3)
- -3 = a . 3
- a = -3/3 = -1
- y = -1 (x2 + 4x + 3)
- y = -x2 – 4x – 3
Berdasarkan persamaan fungsi kuadrat diatas kita ketahui a = -1, b = -4 dan c = -3 atau a < 0, b < 0 dan c < 0. Jadi jawaban soal ini adalah A.
Contoh soal fungsi kuadrat nomor 17
Perhatikan gambar dibawah ini.
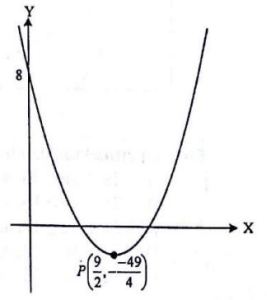
Koordinat titik potong grafik dengan sumbu X adalah…
A. (-1, 0) dan (-8, 0)
B. (-1, 0) dan (8, 0)
C. (1, 0) dan (-8, 0)
D. (1, 0) dan (8, 0)
E. (2, 0) dan (5, 0)
Pembahasan / penyelesaian soal
Berdasarkan grafik fungsi kuadrat diatas kita ketahui:
- titik balik xp = 9/2
- titik balik yp = -49/4
- y = 8
Sehingga kita dapat a =
yp =
b2 – 4 . a . c = 49
92 – 4 . 1 . c = 49
81 – 4c = 49 atau 4c = 81 – 49 = 32
c =
Jadi persamaan fungsi kuadrat grafik diatas adalah:
y = ax2 + bx + c
y = xp – 9x + c
Untuk menentukan titik potong x kita lakukan pemfaktoran sebagai berikut:
xp – 9x + 8 = 0
(x1 – 8) (x2 – 1) = 0
x1 = 8 dan x2 = 1
Jadi titik potong sumbu X adalah (8,0) dan (1,0). Soal ini jawabannya D.
Contoh soal fungsi kuadrat nomor 18
Diketahui f(x) = x2 + 4x – 5, maka nilai minimumnya adalah …
A. -17
B. -9
C. -5
D. -2
E. 4
Pembahasan / penyelesaian soal
Tentukan terlebih dahulu titik ekstrem dengan mengunakan rumus sebagai berikut.
→ y = –→ y = –
→ y = –
Jadi soal ini jawabannya B.
Contoh soal fungsi kuadrat nomor 19
Nilai maksimum dari fungsi kuadrat f(x) = -x2 + 2x + 15 adalah …
A. -32
B. -16
C. 1
D. 16
E. 32
Pembahasan / penyelesaian soal
Cara menghitung nilai maksimum fungsi kuadrat dengan menggunakan rumus dibawah ini.
→ y = –→ y = –
→ y = –
→ y =
Soal ini jawabannya D.
Contoh soal fungsi kuadrat nomor 20
Sebuah peluru ditembakkan vertikal dengan persamaan lintasan h(t) = 150t – 5t2. Tinggi maksimum peluru adalah …
A. 925 m
B. 1.015 m
C. 1.025 m
D. 1.125 m
E. 1.225 m
Pembahasan / penyelesaian soal
→ y = –→ y = –
→ y = –
→ y =
Soal ini jawabannya D.
Contoh soal fungsi kuadrat nomor 21
Diketahui jumlah 2 bilangan adalah 72. Hasil kali maksimum kedua bilangan adalah…
A. 72
B. 144
C. 360
D. 1.296
E. 5.184
Pembahasan / penyelesaian soal
Untuk menjawab soal ini kita lalukan pemisalan 2 bilangan yaitu x dan y sehingga kita peroleh:
- x + y = 72
- y = 72 – x
- x . y = x (72 – x) = 72x – x2
- K = -x2 + 72x
Berdasarkan fungsi kuadrat diatas kita ketahui a = -1, b = 72 dan c = 0. Hasil kali maksimum kita gunakan rumus dibawah ini:
K =K =
Jadi soal ini jawabannya D.
Contoh soal fungsi kuadrat nomor 22
Dua bilangan selisihnya 30. Agar hasil kalinya minimum maka kedua bilangan tersebut adalah…
A. 15 dan -15
B. 20 dan -10
C. 25 dan -5
D. 40 dan 10
E. 50 dan 20
Pembahasan / penyelesaian soal
Kita misalkan kedua bilangan tersebut x dan y maka kita peroleh:
- x – y = 30
- y = x – 30
- K = x . y = x . (x – 30) = x2 – 30x
Berdasarkan fungsi kuadrat diatas kita ketahui a = 1, b = -30 dan c = 0. Maka untuk menentukan nilai minimum kita gunakan rumus dibawah ini.
K =K =
K = -225 dan K = x2 – 30x maka kita dapat:
x2 – 30 x = -225x2 – 30x + 225 = 0
(x – 15)2 = 0
x = 15
Kita subtitusi x = 15 ke persamaan y = x – 30 maka kita peroleh y = 15 – 30 = -15. Jadi hasil perkalian minimum jika kedua bilangan tersebut adalah 15 dan -15.
Jadi soal ini jawabannya A.
Contoh soal fungsi kuadrat nomor 23
Diketahui persegipanjang dengan keliling 64 cm. Agar luas persegi panjang maksimum maka besar panjang dan lebarnya adalah…
A. 64 cm dan 1 cm
B. 32 cm dan 2 cm
C. 32 cm dan 4 cm
D. 16 cm dan 16 cm
E. 16 cm dan 8 cm
Pembahasan / penyelesaian soal
Untuk menyelesaikan soal ini kita misalkan panjang = P dan lebar = L maka kita peroleh:
- 2 (P + L) = 64
- P + L = 32
- P = 32 – L
- Luas = P . L = (32 – L) . L = 32 L – L2
- Luas = L2 – 32L
Dari fungsi kuadrat luas diatas kita ketahui a = 1, b = -32 dan c = 0. Selanjutnya kita menentukan luas maksimum dengan cara dibawah ini:
Luas =Luas =
Luas = -256 dan Luas = L2 – 32L sehingga kita peroleh hubungan sebagai berikut:
- L2 – 32L = – 256
- L2 – 32L + 256 = 0
- (L – 16)2 = 0
- L = 16
L = 16 kita subtitusi ke persamaan L + P = 32 maka P = 32 – L = 32 – 16 = 16. Jadi panjang dan lebar persegi panjang agar maksimum adalah P = 16 cm dan L = 16 cm. Jadi soal ini jawabannya D.