Contoh soal pertidaksamaan nilai mutlak dan penyelesaiannya + pembahasan

Pada postingan ini kita membahas contoh soal pertidaksamaan nilai mutlak dan penyelesaiannya + pembahasannya. Berdasarkan konsep nilai mutlak dan persamaan nilai mutlak, kita akan mempelajari bagaimana konsep pertidaksamaan nilai mutlak. Dalam kehidupan sehari-hari, banyak kita jumpai kasus yang melibatkan pembatasan suatu hal. Seperti lowongan kerja yang mensyaratkan pelamar dengan batas usia tertentu, batas nilai cukup seorang pelajar agar dinyatakan lulus dari ujian dan batas berat bersih suatu kendaraan yang diperbolehkan oleh dinas perhubungan.

Lalu bagaimana cara menyelesaikan soal-soal pertidaksamaan nilai mutlak ?. Jawabannya adalah dengan menggunakan sifat pertidaksamaan nilai mutlak. Untuk setiap nilai a, x bilangan real, maka berlaku sifat pertidaksamaan nilai mutlak sebagai berikut.

Jika a ≥ 0 dan |x| ≤ a, maka -a ≤ x ≤ a
Jika a < 0 dan |x| ≤ a, maka tidak ada bilangan real yang memenuhi pertidaksamaan.
Jika |x| ≥ a dan a > 0 maka x ≥ a atau x ≤ -a.

Contoh soal pertidaksamaan nilai mutlak

Contoh soal 1

Nilai-nilai x yang memenuhi |x| < 3 adalah …
A. x < -3
B. x < 3
C. 0 < x < 3
D. -3 < x < 0
E. -3 < x < 3

Penyelesaian soal / pembahasan

Dengan menggunakan sifat pertidaksamaan nilai mutlak yang pertama diperoleh hasil sebagai berikut.

-a < x < a
-3 < x < 3

Soal ini jawabannya E.

Contoh soal 2

Nilai x yang memenuhi pertidaksamaan |3x – 4| < 8 adalah …
A. x < $\frac {4} {3}$
B. – $\frac {4} {3}$ < x < 4
C. x > $\frac {4} {3}$
D. x > 4
E. x ≠ 0

Penyelesaian soal / pembahasan

Untuk menjawab soal ini kita gunakan sifat pertidaksamaan nilai mutlak yang pertama yaitu sebagai berikut.

-8 < 3x – 4 < 8
– 8 + 4 < 3x < 8 + 4
-4 < 3x < 12
– $\frac {4} {3}$ < x < $\frac {12} {3}$
– $\frac {4} {3}$ < x < 4

Soal ini jawabannya B. Selain itu, soal nomor 2 dapat dijawab dengan cara sebagai berikut:

|3x – 4| < 8
(3x – 4)² < 8²
9x² – 24x + 16 < 64
9x² – 24x -+16 – 64 < 0
9x² – 24x – 48 < 0
3x² – 8x – 16 < 0
(3x + 4) (x – 4) < 0
x = – $\frac {4} {3}$ atau x = 4

Kemudian dibuat garis bilangan dan hasilnya sebagai berikut.

Pertidaksamaan nilai mutlak — Garis bilangan pertidaksamaan nilai mutlak soal nomor 2

Jadi penyelesaiannya adalah – $\frac {4} {3}$ < x < 4. Kita lihat cara pertama dan cara kedua mendapatkan hasil yang sama.

Contoh soal 3

Nilai-nilai x yang memenuhi pertidaksamaan |x – 1| < 2 adalah …
A. x ≤ 1
B. x ≤ 3
C. x > -1
D. -3 < x < 1
E. -1 < x < 3

Penyelesaian soal / pembahasan

Dengan menggunakan sifat pertama pertidaksamaan nilai mutlak diperoleh hasil sebagai berikut.

-2 < x – 1 < 2
-2 + 1 < x < 2 + 1
-1 < x < 3

Soal ini jawabannya E.

Contoh soal 4

Himpunan penyelesaian pertidaksamaan |3x + 2| > 5 adalah…
A. {x|x < – $\frac {1} {3}$ atau x > 0}
B. {x|x < – $\frac {7} {3}$ atau x > 1}
C. {x|x < -1 atau x > 1}
D. {x|x < – $\frac {1} {2}$ atau x > 1}
E. {x|x < – $\frac {1} {4}$ atau x > 0}

Penyelesaian soal / pembahasan

Dengan menggunakan sifat pertidaksamaan nilai mutlak yang ketiga diperoleh hasil sebagai berikut.

3x + 2 < -5 atau 3x + 2 > 5
3x < -5 – 2 atau 3x > 5 – 2
3x < -7 atau 3x > 3
x < – $\frac {7} {3}$ atau x > $\frac {3} {3}$
x < – $\frac {7} {3}$ atau x > 1

Soal ini jawabannya B.

Contoh soal 5

Agar pertidaksamaan |2x – 2| ≥ 10 benar, maka nilai x haruslah …
A. x ≤ 4
B. x ≥ 6
C. x ≤ -4 atau x ≥ 6
D. -4 ≤ x ≤ 6
E. 4 < x < 5

Penyelesaian soal / pembahasan

Dengan menggunakan sifat pertidaksamaan nilai mutlak yang ketiga diperoleh hasil sebagai berikut.

2x – 2 ≤ -10 atau 2x – 2 ≥ 10
2x ≤ -10 + 2 atau 2x ≥ 10 + 2
2x ≤ -8 atau 2x ≥ 12
x ≤ – 4 atau x ≥ 6

Soal ini jawabannya C.

Contoh soal 6

Penyelesaian |7x – 12| – 1 > 8 adalah …
A. x < – $\frac {3} {7}$ atau x > 3
B. x < -3 atau x > $\frac {3} {7}$
C. x < $\frac {3} {7}$ atau x > 3
D. x < $\frac {3} {7}$
E. x > 3

Penyelesaian soal / pembahasan

Untuk menjawab soal ini kita gunakan syarat pertidaksaman nilai mutlak yang ketiga yaitu sebagai berikut.

|7x – 12| > 8 + 1
|7x – 12| > 9
7x – 12 < -9 atau 7x – 12 > 9
7x < -9 + 12 atau 7x > 9 + 12
7x < 3 atau 7x > 21
x < $\frac {3} {7}$ atau x > $\frac {21} {7}$
x < $\frac {3} {7}$ atau x > 3

Soal ini jawabannya C.

Contoh soal 7

Nilai-nilai x yang memenuhi |x + 3| ≤ |2x| adalah …
A. x ≤ – 1 atau x ≥ 3
B. x ≤ – 1 atau x ≥ 1
C. x ≤ – 3 atau x ≥ -1
D. x ≤ 1 atau x ≥ 3
E. x ≤ – 3 atau x ≥ 1

Penyelesaian soal / pembahasan

Cara menjawab soal ini sebagai berikut.

(x + 3)² ≤ (2x)²
x² + 6x + 9 ≤ 4x²
x² – 4x² + 6x + 9 ≤ 0
-3x² + 6x + 9 ≤ 0 (dibagi -3)
x² – 2x + 3 ≥ 0
(x – 3) (x + 1) ≥ 0
x = 3 atau x = -1

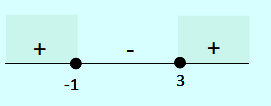
Jadi nilai x yang memenuhi adalah x ≤ -1 atau x ≥ 3. Soal ini jawabannya A.

Contoh soal 8

Nilai-nilai x yang memenuhi pertidaksamaan nilai mutlak |x + 2| ≥ |2x – 2| adalah …
A. 0 ≤ x ≤ 4
B. x ≤ 0 atau x ≥ 4
C. x ≤ – 4 atau x ≥ 0
D. x ≤ 0
E. x ≤ 4

Penyelesaian soal / pembahasan

Cara menyelesaikan soal ini sebagai berikut:

(x + 2)² ≥ (2x – 2)².
x² + 4x + 4 ≥ 4x² – 8x + 4.
x² + 4x + 4 – 4x² + 8x – 4 ≥ 0
-3x² + 12x ≥ 0.
x (-3x + 12) ≥ 0
x = 0 atau x = 4

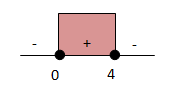
Jadi penyelesaian |x + 2|≥ |2x – 2| adalah 0 ≤ x ≤ 4. Soal ini jawabannya A.

Contoh soal 9

Nilai x yang memenuhi pertidaksamaan nilai mutlak |x + 5| ≤ |1 – 9x| adalah …
A. x ≤ – $\frac {2} {5}$ atau x ≥ $\frac {3} {4}$
B. x ≤ – $\frac {3} {4}$ atau x ≥ $\frac {2} {5}$
C. x ≤ $\frac {2} {5}$ atau x ≥ – $\frac {3} {4}$
D. $\frac {2} {5}$ ≤ x ≤ $\frac {3} {4}$
E. – $\frac {2} {5}$ ≤ x ≤ $\frac {3} {4}$

Penyelesaian soal / pembahasan

(x + 5)² ≤ (1 – 9x)²
x² + 10x + 25 ≤ 1 – 18x + 81x²
x² – 81x² + 10x + 18x + 25 – 1 ≤ 0
80x² – 28x – 24 ≥ 0
20x² – 7x – 6 ≥ 0
(4x – 3) (5x + 2) ≥ 0
x = $\frac {3} {4}$ atau x = – $\frac {2} {5}$

Dengan menggunakan garis bilangan diperoleh penyelesaiannya.

Jadi penyelesaiannya adalah x ≤ – $\frac {2} {5}$ atau x ≥ $\frac {3} {4}$ . Soal ini jawabannya A.

Contoh soal 10

Selesaikan pertidaksamaan nilai mutlak |2x + 2| > x – 4.

Penyelesaian soal / pembahasan

Berdasarkan definisi persaman nilai mutlak kita peroleh:

|2x + 2| = 2x + 2 jika x ≥ -1
|2x + 2| = -(2x + 2) jika x < -1

Untuk x ≥ -1 kita peroleh:

2x + 2 > x – 4
2x + 2 – x + 4 > 0
x + 6 > 0
x > -6

Untuk x < -1 kita peroleh:

– (2x + 2) > x – 4
-2x – 2 – x + 4 > 0
-3x + 2 > 0
– x > – 2/3
x < 2/3

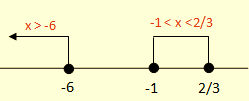
Jadi penyelesaian pertidaksamaan nilai mutlak |2x + 2|> x – 4 adalah x > – 6 atau -1 < x < 2/3.

Contoh soal pertidaksamaan nilai mutlak dan penyelesaiannya + pembahasan

Contoh soal pertidaksamaan nilai mutlak

Tinggalkan Balasan Batalkan balasan