Contoh soal sudut luar segitiga dan pembahasan

Pada artikel ini kita akan mempelajari sudut luar segitiga. Agar kalian lebih paham, perhatikan gambar segitiga ABC dan sudut-sudutnya dibawah ini.

Berdasarkan gambar segitiga diatas, ∠A₁, ∠B₁, dan ∠C₁ disebut dengan sudut luar segitiga. Hal ini karena ketiga sudut tersebut terletak diluar segitiga ABC. Sedangkan ∠A₂, ∠B₂ dan ∠C₂ disebut sudut dalam segitiga, karena terletak didalam segitiga ABC.

Setelah kalian mengetahui sudut luar suatu segitiga, yang menarik diperhatikan selanjutnya adalah berapa besar sudut-sudut luar segitiga tersebut. Untuk menjawab pertanyaa tersebut, perhatikan kembali segitiga ABC diatas.

Pada titik C terdapat dua buah sudut yaitu ∠C₁ dan ∠C₂ yang saling berpelurus. Jumlah sudut dalam segitiga adalah 180° sehingga diperoleh persamaan sebagai berikut.

• ∠C₁ + ∠C₂ = 180° …….. (1)
• ∠A₂ + ∠B₂ + ∠C₂ = 180° …….. (2)

Dari persamaan (1) dan (2) diperoleh:

• ∠A₂ + ∠B₂ = 180° – ∠C₂
• ∠C₁ = 180° – ∠C₂
• ∠A₂ + ∠B₂ = ∠C₁

Contoh soal sudut luar segitiga

Contoh soal 1

Diketahui ∠A = 60° dan ∠ = 58°. Besar ∠BCD adalah …
A. 42°
B. 62°
C. 108°
D. 118°

Pembahasan

Sudut BCD = ∠C.

• ∠C = ∠A + ∠B
• ∠C = 60° + 58° = 118°

Soal ini jawabannya D.

---

Contoh soal 2

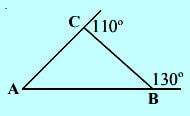
Dari gambar diatas, ∠A = …
A. 50°
B. 60°
C. 70°
D. 80°

Pembahasan

• ∠B = 180° – 130° = 50°
• ∠A + ∠B = 110°
• ∠A = 110° – ∠B
• ∠A = 110° – 50° = 60°

Soal ini jawabannya B.

---

Contoh soal 3

Pada gambar diatas, diketahui ∠A = (2x + 2)°, ∠B = (3x – 2)° dan ∠BCD = (6x – 25)°. Besar ∠ACB adalah …
A. 25°
B. 50°
C. 55°
D. 125°

Pembahasan

Tentukan terlebih dahulu nilai x.

• ∠A + ∠B = ∠BCD
• 2x + 2 + 3x – 2 = 6x – 25
• 5x = 6x – 25
• 5x – 6x = -25
• x = 25

Selanjutnya menentukan besar ∠BCD.

• ∠BCD = 6x – 25
• ∠BCD = 6 . 25 – 25 = 125°

Maka besar ∠ACB sebagai berikut.

• ∠ACB + ∠BCD = 180°
• ∠ACB = 180° – ∠BCD
• ∠ACB = 180° – 125° = 55°

Soal ini jawabannya C.

---

Contoh soal 4

Besar sudut A pada gambar berikut adalah …

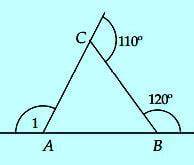
A. 50°
B. 70°
C. 80°
D. 100°

Pembahasan

• ∠B = 180° – 120° = 60°
• ∠A + ∠B = 110°
• ∠A = 110° – ∠B
• ∠A = 110° – 60° = 50°

Soal ini jawabannya A.

---

Contoh soal 5

Pada gambar diatas, ∠A₁ adalah …
A. 100°
B. 110°
C. 130°
D. 150°

Pembahasan

• ∠B = 180° – 120° = 60°
• ∠A + ∠B = 110°
• ∠A = 110° – ∠B
• ∠A = 110° – 60° = 50°
• ∠A₁ = 180° – ∠A
• ∠A₁ = 180° – 50° = 130°

Soal ini jawabannya C.