Contoh soal luas segitiga trigonometri dan penyelesaiannya + pembahasan

Pada postingan ini kita membahas contoh soal cara menghitung luas segitiga trigonometri dan penyelesaiannya + pembahasan. Segitiga tersusun dari tiga buah sisi dan tiga buah sudut. Perhatikan gambar segitiga ABC dibawah. Misalkan panjang AB = c, panjang BC = a, dan panjang AC = b, maka rumus untuk menghitung luas segitiga sebagai berikut.

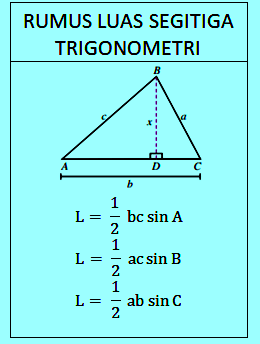
Rumus luas segitiga yang diketahui dua sudut dan panjang salah satu sisinya sebagai berikut.

→ L =

a² sin B sin C

2 sin A

→ L =

b² sin A sin C

2 sin B

→ L =

c² sin A sin B

2 sin C

Rumus luas segitiga jika diketahui ketiga sisinya sebagai berikut.

→ L = √ s (s – a) (s – b) (s – c)  
Dengan s =

1

2

(a + b + c)

Contoh soal luas segitiga trigonometri

Contoh soal 1

Pada ΔPQR diketahui ∠P = 65° dan ∠R = 85^o. Panjang sisi QR 4 cm dan sisi PQ = 8 cm. Luas ΔPQR adalah … cm².
A. 8
B. 16
C. 20
D. 24
E. 32

Penyelesaian soal / pembahasan

Perlu di ingat pada ΔPQR, sisi QR = p, sisi PQ = r dan sisi PR = q. Jadi cara menghitung luas segitiga soal ini sebagai berikut:

• L = 1/2 . p . r . sin Q
• L = 1/2 . QR . PQ . sin (180^o – 65^o – 85^o)
• L = 1/2 . 4 cm . 8 cm . sin 30°.
• L = 16 cm² . 1/2
• L = 8 cm²

Soal ini jawabannya A.

---

Contoh soal 2

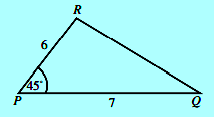
Luas segitiga berikut adalah …

A.
B.
C.
D. 20
E. 20

Penyelesaian soal / Pembahasan

Cara menghitung luas segitiga soal ini sebagai berikut.

• L = 1/2 . q . r . sin P
• L = 1/2 . PR . PQ . sin 45^o
• L = 1/2 . 6 . 7 . 1/2 √ 2  
• L = √ 2  

Soal ini jawabannya B.

---

Contoh soal 3

Pada segitiga KLM diketahui k = 16 cm, l = 10 cm dan luas segitiga 40 cm². Besar sudut apit sisi k dan sisi l adalah …
A. 75^o
B. 60^o
C. 45^o
D. 30^o
E. 15^o

Penyelesaian soal / pembahasan

• L = 1/2 . k . l . sin M
• 40 cm² = 1/2 . 16 cm . 10 cm . sin M
• 40 cm² = 80 cm² . sin M
• sin M = 40/80 = 1/2
• M = 30^o

Soal ini jawabannya D.

---

Contoh soal 4

Luas segitiga yang memiliki panjang sisi masing-masing 28 cm, 26 cm dan 30 cm adalah …
A. 84 cm²
B. 168 cm²
C. 186 cm²
D. 336 cm²
E. 672 cm²

Penyelesaian soal / pembahasan

Pada soal ini diketahui:

• a = 28 cm
• b = 26 cm
• c = 30 cm
• s = 1/2 (28 cm + 26 cm + 30 cm) = 42 cm

Cara menghitung luas segitiga soal ini sebagai berikut.

• L = √ s (s – a) (s – b) (s – c)  
• L = √ 42 (42 – 28) (42 – 26) (42 – 30)  
• L √ 42 . 14 . 16 . 12  
• L = √ 112.896   = 336 cm²

Soal ini jawabannya D.

---

Contoh soal 5

Pada ΔABC ditentukan bahwa a = 18 cm, b = 10 cm dan keliling 40 cm. Luas segitiga tersebut adalah …
A. 40 √ 2   cm²
B. 30 √ 2   cm²
C. 20 √ 2   cm²
D. 10 √ 2   cm²
E. 8 √ 2   cm²

Penyelesaian soal / pembahasan

Pada soal ini diketahui:

• a = 18 cm
• b = 10 cm
• c = 40 cm – 18 cm – 10 cm = 12
• s = 1/2 . 40 cm = 20 cm

Cara menghitung luas segitiga soal ini dengan rumus sebagai berikut.

• L = √ s (s – a) (s – b) (s – c)  
• L = √ 20 (20 – 18) (20 – 10) (20 – 12)  
• L √ 20 . 2 . 10 . 8  
• L = √ 3.200   = 40 √ 2   cm²

Soal ini jawabannya A.

---

Contoh soal 6

Luas segitiga sama sisi yang panjang sisinya 10 cm adalah … cm².
A. 25 √ 2  
B. 25 √ 3  
C. 50
D. 50 √ 3  
E. 100

Penyelesaian soal / pembahasan

Pada soal ini diketahui:

• a = b = c = 10 cm
• s = 1/2 (10 cm + 10 cm + 10 cm) = 15 cm

Cara menghitung luas segitiga soal ini sebagai berikut.

• L = √ s (s – a) (s – b) (s – c)  
• L = √ 15 (15 – 10) (15 – 10) (15 – 10)  
• L √ 15 . 5 . 5 . 5  
• L = √ 3 . 5 . 5 . 5 . 5  = 5 . 5 √ 3   cm²
• L = 25 √ 3   cm²

Soal ini jawabannya B.

---

Contoh soal 7

Hitunglah luas segitiga dibawah ini.

Penyelesaian soal / pembahasan

Rumus menghitung luas segitiga diatas sebagai berikut

→ L =

c² sin A sin B

2 sin C

→ L =

(10 cm)² sin 30^o sin 60^o

2 sin 90^o

→ L =

100 cm² . 1/2 . 1/2 √ 3  

2 . 1

→ L = 12,5 √ 3   cm²

Itulah contoh soal luas segitiga trigonometri dan penyelesaiannya. Semoga penyampaian contoh soal ini mudah dipahami sehingga bermanfaat.