Contoh soal aturan sinus & aturan cosinus & penyelesaiannya + pembahasan

Pada postingan ini kita membahas contoh soal aturan sinus & aturan cosinus dan penyelesaiannya / pembahasannya. Aturan sinus dan cosinus menunjukkan hubungan antara sudut-sudut pada suatu segitiga sembarang. Gambar dibawah menunjukkan segitiga ABC dengan panjang sisi AB = c, BC = a dan AC = b. Sementara itu, CE dan BD adalah garis tinggi segitiga ABC.

Berdasarkan gambar diatas, aturan sinus dinyatakan dengan:

a

sin α

=

b

sin β

=

c

sin γ

Sedangkan aturan cosinus mempunyai tiga persamaan yaitu sebagai berikut.

• a2 = b2 + c2 – 2bc . cos α.
• b2 = a2 + c2 – 2ac . cos β.
• c2 = a2 + b2 – 2ab . cos γ.

Contoh aturan sinus

Contoh soal 1

Perhatikan ΔABC berikut.

Aturan sinus yang berlaku pada segitiga tersebut adalah…
A.

a

b

=

sin α

sin ɡ

B.

b

a

=

sin β

sin ɡ

C.

c

sin ɡ

=

b

sin α

D.

b

sin ɡ

=

c

sin α

E.

b

sin β

=

c

sin α

Penyelesaian soal / Pembahasan

Aturan sinus yang berlaku pada segitiga diatas sebagai berikut.

→

b

sin α

=

c

sin ɡ

→

c

sin ɡ

=

b

sin α

Soal ini jawabannya C.

---

Contoh soal 2

JIka ΔXYZ dengan ∠X = 30^o, ∠Y = 45^o dan x = 8 cm maka sisi y adalah …
A. 4 √ 2  
B. 4 √ 3  
C. 8 √ 2  
D. 8 √ 3  
E. 16 √ 3  

Penyelesaian soal / pembahasan

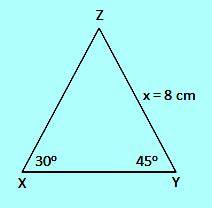
Berdasarkan aturan sinus diperoleh:

→

x

sin X

=

y

sin Y

→

8 cm

sin 30°

=

y

sin 45°

→ y =

8 cm . sin 45^o

sin 30^o

→ y =

8 cm . 1/2 √ 2  

1/2

= 8 √ 2   cm

Soal ini jawabannya C.

---

Contoh soal 3

Diketahui segitiga KLM dengan panjang sisi k = 2 √ 2   cm, l = 4 cm dan ∠K = 30°. Besar sudut ∠L adalah …
A. 15^o
B. 30^o
C. 45^o
D. 60^o
E. 90^o

Penyelesaian soal

Soal ini dapat dijawab dengan langkah-langkah dibawah ini.

→

k

sin K

=

L

sin L

→

2 √ 2  

sin 30°

=

4

sin L

→ sin L =

4 . 1/2

2√

2

=

1

√

2

= 1/2 √ 2   cm

Jadi ∠L = 45°. Soal ini jawabannya C.

---

Contoh soal 4

Diketahui segitiga PQR, panjang sisi QR = 8 cm, ∠P = 45° dan ∠R = 60°, Panjang sisi PQ adalah …
A. 2 √ 6   cm
B. 4 √ 2   cm
C. 4 √ 6   cm
D. 8 √ 3   cm
E. 8 √ 6   cm

Penyelesaian soal / pembahasan

Cara menjawab soal ini sebagai berikut:

→

P

sin P

=

R

sin R

→

8 cm

sin 45°

=

R

sin 60°

→ R =

8 cm . sin 60^o

sin 45^o

→ R =

8 cm . 1/2 √

3

1/2√

2

= 4√

6

cm

Soal ini jawabannya C.

---

Contoh soal aturan cosinus

Contoh soal 1

Pada segitiga ABC diketahui panjang sisi AB = 7 cm, BC = 4 cm dan ∠ABC = 120°. Panjang sisi AC = … cm.
A. √ 37  
B. 7
C. 8
D. √ 93  
E. 7 √ 2  

Penyelesaian soal / pembahasan

Diketahui:

• AB = c = 7 cm
• BC = a = 4 cm
• AC = b = …
• ∠ABC = ∠B = 120^o

Untuk menghitung panjang AC = b menggunakan aturan cosinus sebagai berikut.

• b2 = a2 + c2 – 2 . a . c . cos 120°.
• b2 = 42 + 72 – 2 . 4 . 7 . -1/2.
• b2 = 16 + 49 + 28 = 93.
• b = √ 93   cm.

Jadi soal ini jawabannya D.

---

Contoh soal 2

Seorang seniman membuat ukuran pada pigura seperti gambar berikut.

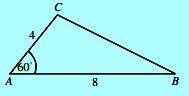
Panjang sisi BC pada pigura adalah …
A. 4
B. 4 √ 2  
C. 4 √ 3  
D. 4 √ 5  
E. 4 √ 7  

Penyelesaian soal / pembahasan

Dengan menggunakaan aturan cosinus diperoleh hasil sebagai berikut.

• a2 = b2 + c2 – 2 . b . c . cos A.
• a2 = 42 + 82 – 2 . 4 . 8 . cos 60^o.
• a² = 16 + 64 – 32.
• a² = 48
• a = √ 48   = √ 16 x 3   = 4 √ 3  

Jadi soal ini jawabannya C.

---

Contoh soal 3

Diketahui ΔPQR dengan panjang PQ = 2 √ 19   cm, QR = 6 cm, dan PR = 4 cm. Besar sudut yang terbesar pada ΔPQR adalah …
A. 30^o
B. 45^o
C. 60^o
D. 120^o
E. 150^o

Penyelesaian soal / Pembahasan

Sudut terbesar berada didepan garis terpanjang yaitu PQ = 2 √ 19   cm. Jadi sudut terbesar adalah sudut R. Dengan menggunakan aturan cosinus nilai sudut R sebagai berikut.

• r2 = p2 + q2 – 2 . p . q . cos R.
• (2 √ 19   )2 = 62 + 42 – 2 . 6 . 4 . cos R.
• 76 = 36 + 16 – 48 . cos R.
• 48 cos R = 36 + 16 – 76 = -24
• 48 cos R = -24
• cos R = -24/48 = -1/2
• R = 120^o

Soal ini jawabannya D.

---

Contoh soal 4

Perhatikan gambar.

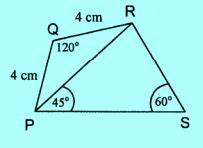
Panjang RS adalah …
A. 4 √ 3   cm
B. 4 √ 2   cm
C. 3 √ 3   cm
D. 2 √ 3   cm
E. 2 √ 2   cm

Penyelesaian soal / Pembahasan

Tentukan panjang PR dengan menggunakan aturan cosinus dibawah ini.

• PR2 = QR2 + PQ2 – 2 . QR . PQ . cos Q.
• PR2 = 42 + 42 – 2 . 4 . 4 . cos 120^o.
• PR² = 16 + 16 + 16.
• PR² = 48
• PR = √ 48   = √ 16 x 3   = 4 √ 3  

Selanjutnya menentukan RS dengan menggunakan aturan sinus dibawah ini.

→

RS

sin P

=

PR

sin S

→

4√

3

cm

sin 60°

=

RS

sin 45°

→ RS =

4√

3

cm . sin 45^o

sin 60^o

→ RS =

4 √

3

cm . 1/2 √

2

1/2√

3

= 4 √

2

cm

Soal ini jawabannya B.

---

Contoh soal 5

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka 120^o sejauh 40 km, kemudian berlayar menuju ke pelabuhan C dengan jurusan 240^o sejauh 80 km. Jarak antara pelabuhan C dan A adalah…
A. 20 √ 3   km
B. 40 km
C. 40 √ 3   km
D. 40 √ 5   km
E. 40 √ 7   km

Penyelesaian soal / pembahasan

Diketahui:

• ∠B = 360^o – 240^o – 60^o = 60^o
• AB = c = 40 km
• BC = a = 80 km

Dengan menggunakan aturan cosinus diperoleh panjang AC = b sebagai berikut.

• b2 = a2 + c2 – 2 . a . c . cos B.
• b2 = (80 km)2 + (40 km)2 – 2 . 80 . 40 . cos 60^o.
• b² = 6400 + 1600 – 3200.
• b² = 4.800
• b = √ 4.800   = √ 1600 x 3   = 40 √ 3 km

Soal ini jawabannya C.