Postingan ini membahas contoh soal dua segitiga sebangun dan kongruen yang disertai jawabannya atau pembahasannya. Dua segitiga dikatakan sebangun jika salah satu syarat dipenuhi yaitu dua sudutnya sama besar, sisi-sisi yang bersesuaian mempunyai perbandingan yang sama, satu sudut dan dua sisi yang mengapit sudut itu mempunyai perbandingan yang sama.
Contoh soal 1
Perhatikan gambar berikut.
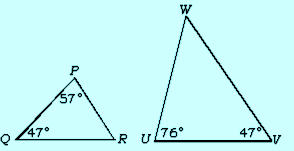
- Hitunglah ∠R dan ∠ W pada gambar diatas.
- Buktikan bahwa kedua segitiga tersebut sebangun.
- Tulislah perbandingan senilai sisi-sisi yang bersesuaian.
Jawaban
Jawaban soal 1:
∠R = 180° – 57° – 47° = 76°
∠W = 180° – 76° – 47° = 57°
Jawban soal 2:
Kedua segitiga sebangun karena dua sudutnya sama besar yaitu ∠ P = ∠ W = 57° dan ∠Q = ∠V = 47°
Jawaban soal 3:
QR
UV = PQ
VW = PR
WU
Contoh soal 2

- Apakah pasangan segitiga pada gambar (a) diatas sebangun?. Bagaimana pasangan segitiga pada gambar (b) apakah juga sebangun?.
- Jika sebangun, sebutkan pasangan sudut-sudut yang sama besar?.
Jawaban
Jawaban soal 1:
Gambar (a) :
HI
JK = 9
6 = 3
2
GI
KL = 4,5
3 = 3
2
GH
JL = 6
4 = 3
2
Karena mempunyai perbandingan yang sama maka gambar (a) adalah dua segitiga sebangun.
Gambar b:
ST
XZ = 21
9 = 7
3
RT
XY = 18
8 = 9
4
RS
YZ = 15
5 = 3
1
Karena perbandingannya berbeda maka segitiga gambar (b) tidak sebangun
Jawaban soal 2:
∠H = ∠J (karena HJ/GH = JK/JL = 3/2).
∠I = ∠K (karena GI/HI = KL/JK = 1/2).
Contoh soal 3
Perhatikan gambar berikut.
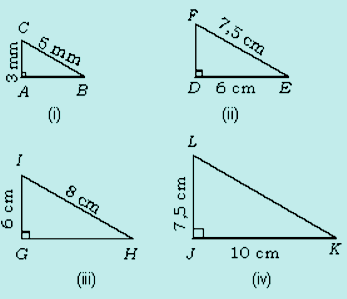
- Hitunglah panjang sisi yang belum diketahui pada keempat segitiga tersebut.
- Segitiga mana saja yang sebangun dengan segitiga BAC?
Jawaban
Jawaban soal 1:
AB = 4 cm (menggunakan tripel pythagoras 3, 4, 5)
DF2 = (7,5)2 – 62 = 56,25 – 36 = 20,25
DF = √ 20,25 = 4,5
GH2 = 82 – 62 = 64 – 36 = 28
GH = √ 28
KL2 = 102 + 7,52 = 100 + 56,25 = 156,25
KL = √ 156,25 = 12,5
Jawaban soal 2:
BAC ∼ DEF ∼JKL (karena perbandingan sisi-sisi yang bersesuaian sama besar).
Contoh soal 4

- Buktikan bahwa segitiga ABE dan segitiga CDE sama sudut!.
- Jika panjang AB = 6 cm, AE = 7,5 cm, ED = 5 cm dan EC = 3 cm, hitunglah panjang BE dan CD.
Jawaban
Jawaban soal 1:
Sudut AEB = sudut CED (karena bertolak belakang)
Sudut A = sudut D dan sudut B = sudut C (karena dalam berseberangan)
Karena sudut-sudutnya sama maka segitiga AEB dan CED sebangun
Jawaban soal 2:
BE
AE = EC
ED
BE
7,5 = 3
5
BE = 3
5 x 7,5 = 4,5
AE
AB = ED
CD
7,5
6 = 5
CD
CD = 6
7,5 x 5 = 4
Contoh soal 5
Pada gambar segitiga CDE berikut ini, garis PG // CD.

- Sebutkan sudut-sudut yang sama besar pada ∆FGE dan ∆CDE beserta alasannya.
- Tulislah perbandingan senilai sisi-sisi yang bersesuaian.
- Jika panjang FG = 8 cm, GE = 9 cm, DG = 3 cm, dan CE = 8 cm, hitunglah panjang CD, FE dan CF.
Jawaban
Jawaban soal 1 :
∠CDG = ∠FGE dan ∠GFE = ∠DCF (karena sudut-sudut yang sehadap).
Jawaban soal 2:
EF
EC EG
ED = FG
CD
Jawaban soal 3:
GE
DE = FG
CD
9
12 = 8
CD
CD = 12/9 x 8 = 10,67 cm
FE
CE = GE
DE
FE
8 = 9
12
FE = 9/12 x 8 = 6 cm
CF = CE – FE = 8 – 6 = 2 cm
Contoh soal 6
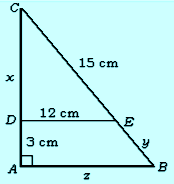
Pada gambar diatas, segitiga ABC siku-siku di A dan DE sejajar AB. Hitunglah panjang x, y dan z.
Jawaban
x2 = 152 – 122 = 225 – 144 = 81
x = 9
x/AC = EC/BC
9/12 = 15/BC
BC = 12/9 x 15 = 20
y = BC – EC = 20 cm – 15 cm = 5 cm
EC/BC = DE/z
15/20 = 12/z
z = 20/15 x 12 = 16 cm.
Jadi x = 9, y = 5 cm dan z = 16 cm
Contoh soal 7

Gambar diatas adalah segitiga PQR dengan panjang QS = 12 cm, dan RS = 9 cm. Tentukan panjang PS, PQ, dan QR.
Jawaban
QS adalah tinggi segitiga PQR sehingga:
QS2 = RS . PS
122 = 9 . PS atau 144 = 9 . PS
PS = 144/9 = 16 cm
PQ2 = PS . PR = 16 . (16 + 9) = 16 . 25
PQ = √ 16 . 25 = 4 . 5 = 20 cm
QR2 = RS . PR = 9 . (16 + 9) = 9 . 25
QR = √ 9 . 25 = 3 . 5 = 15 cm
Contoh soal 8
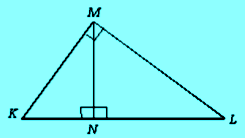
Segitiga KLM merupakan segitiga siku-siku di M, KN = 9 cm dan NL = 16 cm. Tentukan panjang MN, MK, dan ML.
Jawaban
MN2 = KN . NL = 9 . 16
MN = √ 9 . 16 = 3 . 4 = 12 cm
MK2 = KN . KL = 9 . (9 + 16) = 9 . 25
MK = √ 9 . 25 = 3 . 5 = 15 cm
ML2 = NL . KL = 16 . (16 + 9) = 16 . 25
ML = 4 . 5 = 20 cm
Contoh soal 9
Tentukan nilai a, b, c dan d.

Jawaban
a =
b . 10 = 6 . (b + 3)
10b = 6b + 18
10b – 6b = 18 atau 4b = 18 sehingga b = 18/4 = 4,5
c = 4,5/9 . 8 = 4
d = 6/9 . 8 = 5,33
Jadi a = 15, b = 4,5, c = 4 dan d = 5,33.
Contoh soal 10
Tentukan nilai x, y dan z.

Jawaban
y =
x =
12 + z =
z = 21,15 – 12 = 9,15