Postingan ini berisi pembahasan soal UN atau Ujian Nasional matematika SMA program IPA tahun 2019 bagian satu. Jumlah soal yang dibahas yaitu 15 soal dimulai dari nomor 1 hingga nomor 15. Postingan ini dapat digunakan sebagai bahan belajar dalam menghadapi UN matematika tahun depan dan selanjutnya.
Soal 1 – Perhatikan gambar grafik berikut:

Jika grafik fungsi f(x) = ax2 + bx + c seperti gambar, nilai a, b, dan c yang memenuhi adalah …
A. a > 0, b > 0 dan c > 0
B. a < 0, b > 0, dan c > 0
C. a < 0, b > 0 dan c < 0
D. a > 0, b < 0, dan c > 0
E. a < 0, b < 0, dan c < 0
Pembahasan
Cara menjawab soal ini kita bentuk persamaan fungsi kuadrat dengan cara sebagai berikut:
y = a (x – x1) (x – x2)
y = a (x – (-3)) (x – (-1))
y = a (x + 3) (x + 1)
y = a (x2 + 4x + 3)
3 = a (02 + 4 . 0 + 3)
a = 3/3 = 1
y = x2 + 4x + 3
Berdasarkan persamaan fungsi kuadrat diatas kita peroleh a = 1 (a > 0), b = 4 (b > 0) dan c = 3 (c > 0). Jadi soal ini jawabannya A.
Soal 2 – Harga 3 buah buku dan 2 buah penggaris Rp 18.000,00. Jika harga sebuah buku Rp 1.000,00 lebih mahal dari sebuah penggaris, harga 2 buah buku dan 5 buah penggaris adalah…
A. Rp 19.000,00
B. Rp 23.000,00
C. Rp 25.000,00
D. Rp 27.000,00
E. Rp 30.000,00
Pembahasan
Misalkan buku = x dan penggaris = y maka kita peroleh:
3x + 2y = 18.000 (persamaan 1)
x = y + 1.000 (persamaan 2)
Subtitusi persamaan 2 ke persamaan 1:
3 (y + 1000) + 2y = 18.000
3y + 3000 + 2y = 18.000
5y = 15.000
y = 15.000/5 = 3.000
x = y + 1000 = 3000 + 1000 = 4000
Jadi harga 2 buku dan 5 penggaris = 2x + 5y = 2 . 4000 + 5 . 3000 = 8.000 + 15.000 = Rp 23.000,00. Soal ini jawabannya B.
Soal 3 – Daerah yang memenuhi sistem pertidaksamaan linear 3x + 4y ≤ 96; x + y ≤ 30 ; x ≥ 0 ; y ≥ 0 adalah…

A. I
B. II
C. III
D. IV
E. V
Pembahasan
Karena notasi pertidaksamaan kedua garis kurang dari sama dengan (3x + 4y ≤ 96 dan x + y ≤ 30) maka daerah yang memenuhi pertidaksamaan terletak di ruang ke IV. Jadi soal ini jawabannya D.
- Ruang I = 3x + 4y ≤ 96; x + y ≥ 30 ; x ≥ 0 ; y ≤ 0
- Ruang II =3x + 4y ≥ 96; x + y ≥ 30 ; x ≥ 0 ; y ≤ 0
- Ruang III = 3x + 4y ≥ 96; x + y ≥ 30 ; x ≥ 0 ; y ≥ 0
- Ruang IV = 3x + 4y ≤ 96; x + y ≤ 30 ; x ≥ 0 ; y ≥ 0
- Ruang V = 3x + 4y ≥ 96; x + y ≤ 30 ; x ≥ 0 ; y ≥ 0
Soal 4 – Daerah yang diarsir pada gambar dibawah ini adalah daerah penyelesaian dari pertidaksamaan…

A. A. 6x + y ≤ 12 ; 5x + 4y ≥ 20 ; x ≥ 0 ; y ≥ 0
B. 6x + y ≥ 12 ; 5x + 4y ≥ 20 ; x ≥ 0 ; y ≥ 0
C. 6x + y ≤ 12 ; 5x + 4y ≤ 20 ; x ≥ 0 ; y ≥ 0
D. x + 6y ≤ 12 ; 4x + 5y ≥ 20 ; x ≥ 0 ; y ≥ 0
E. x + 6y ≥ 12 ; 5x + 4y ≤ 20 ; x ≥ 0 ; y ≥ 0
Pembahasan
Tentukan terlebih dahulu persaman kedua garis grafik diatas dengan rumus dibawah ini:
Persamaan garis 1 dengan titik potong (4 ; 0) dan (0 ; 5):
4y + 5x = 20
Persamaan garis 2 dengan titik potong (2 ; 0) dan (0 ; 12):
2y + 12x = 24 atau 6x + y = 12
Kemudian kita ganti notasi sama dengan (=) dengan pertidaksamaan sesuai daerah yang diarsir (lihat nomor 3 diatas = ruang ke V). Jadi pertidaksamaan yang sesuai adalah 6x + y ≤ 12 ; 5x + 4y ≥ 20 ; x ≥ 0 ; y ≥ 0. Soal ini jawabannya A.
Soal 5 – Seorang pedagang beras akan membuat beras campuran dengan cara mencampur beras jenis A dan beras jenis B. Beras campur pertama terdiri dari 4 kg beras jenis A dan 8 kg beras jenis B, sedangkan beras campur kedua terdiri dari 8 kg beras jenis A dan 10 kg beras jenis B. Beras yang tersedia untuk beras jenis A dan B berturut-turut 80 ton dan 106 ton. Jika harga jual untuk beras campuran jenis pertama Rp 60.000,00 dan jenis kedua Rp 80.000,00 penjualan maksimum yang diperoleh adalah…
A. Rp 1.200.000.000,00
B. Rp 920.000.000,00
C. Rp 840.000.000,00
D. Rp 800.000.000,00
E. Rp 795.000.000,00
Pembahasan
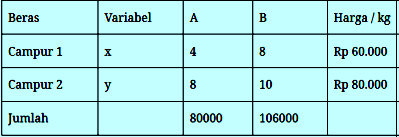
Model matematika soal diatas:
4x + 8y ≤ 80.000 ; 8x + 10y ≤ 106000 ; x ≥ 0 ; y ≥0
atau x + 2y ≤ 20000 ; 4x + 5y ≤ 53000 ; x ≥ 0 ; y ≥0
Fungsi objektif: 60.000 x + 80.000 y
Titik potong garis x + 2y = 20000 adalah (0 ; 10000) dan (20000 ; 0)
Titik potong garis 4x + 5y = 53000 adalah (0 ; 10600) dan (13250 ; 0)
Titik potong kedua garis:

x + 2y = 20000
x = 20000 – 2y = 20000 – 2 . 9000 = 2000


Nilai yang terbesar atau maksimum adalah 840 juta. Soal ini jawabannya C.
Soal 6 – Seorang peternak ayam petelur mencatat telur yang dihasilkan selama 12 hari. Setiap hari banyaknya telur yang dihasilkan bertambah 4 buah. Jika hari pertama telur yang dihasilkan berjumlah 20 buah, jumlah seluruh telur selama 12 hari adalah…
A. 480
B. 496
C. 504
D. 512
E. 520
Pembahasan
Sn = n
2
(2a + (n – 1) b)
S12 = 12
2
(2 . 20 + (12 – 1) 4) = 504
Soal ini jawabannya C.
Soal 7 – Seorang peneliti melakukan pengamatan terhadap bakteri tertentu. Setiap 1/2 hari bakteri membelah diri menjadi 2. Pada awal pengamatan terdapat 2 bakteri. Jika setiap 2 hari 1/4 dari jumlah bakteri mati, banyak bakteri setelah 3 hari adalah…
A. 48 bakteri
B. 64 bakteri
C. 96 bakteri
D. 128 bakteri
E. 192 bakteri
Pembahasan
Jumlah bakteri hari 1 = U3 = arn – 1 = 2 . 23 – 1 = 8
Jumlah bakteri hari 2 = U3 – 1/4 U3 = 8 . 23 – 1 – 1/4 . 8 . 23 – 1
Jumlah bakteri hari 2 = 8 . 4 – 1/4 . 8 . 4 = 32 – 8 = 24
Jumlah bakteri hari 3 = 24 . 23 – 1 = 24 . 4 = 96
Soal ini jawabannya C.
Soal 8 – Sebuah bola tenis dijatuhkan dari ketinggian 2 m dan memantul kembali dengan ketinggian 3/4 tinggi sebelumnya. Pemantulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah…
A. 12 m
B. 14 m
C. 16 m
D. 18 m
E. 20 m
Pembahasan
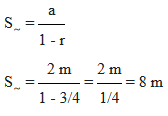
Panjang lintasan bola tenis ketika dijatuhkan adalah panjang lintasan ketika jatuh dan panjang lintasan setelah jatuh. Artinya panjang lintasannya 2 kali kecuali ketika dijatuhkan pertama kali. Jadi panjang lintasan seluruhnya = 2 . 8 m – 2 m = 16 m – 2 m = 14 m. Soal ini jawabannya B.

A. {x|1 ≤ x < 4, x ∈ R}
B. {x|x ≤ -1 atau 3 ≤ x < 4, x ∈ R}
C. {x|x ≤ -3 atau 1 ≤ x < 4, x ∈ R}
D. {x|1 ≤ x ≤ 3 atau x > 4, x ∈ R}
E. {x|-3 ≤ x ≤ 1 atau x > 4, x ∈ R}
Pembahasan
Syarat agar akar terdefinisi adalah tidak negatif dan penyebut tidak nol atau x ≠ 4 . Artinya harus lebih besar sama dengan nol.

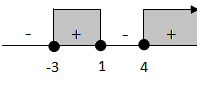
Berdasarkan garis bilangan diatas maka himpunan penyelesaiannya adalah -3 ≤ x ≤ 1 atau x > 4. Jadi soal ini jawabannya E.
Soal 10 – Diketahui f : R → R dan g : R → R dengan (f o g) (x) = 8x3 – 20x2 + 22x – 10 dan g(x) = 2x – 1. Nilai dari f(1) = …
A. -10
B. -1
C. 0
D. 1
E. 10
Pembahasan
(f o g)(x) = f(g(x)) = f(2x – 1)
2x – 1 = 1 maka 2x = 1 + 1 = 2
x = 2/2 = 1
f(1) = 8 . 13 – 20 . 12 + 22 . 1 – 10
f(1) = 8 – 20 + 22 – 10 = 0
Soal ini jawabannya C.
Soal 11 – Diketahui fungsi f(x) = √ 3x + 5 dengan x ≥ -5/3. Jika f-1 (x) adalah invers dari fungsi f(x), nilai dari f-1 (3) = …
A. 4/3
B. 2/3
C. 1/3
D. -2/3
E. -4/3
Pembahasan
y = √ 3x + 5y2 = 3x + 5
3x = y2 – 5
x =
f-1 (x) =
f-1 (3) =
Soal ini jawabannya A.
Soal 12 – Diketahui persamaan matriks:

Nilai 2a – b = …
A. 18
B. 16
C. 14
D. 10
E. 6
Pembahasan
Berdasarkan perkalian matriks diperoleh:

Jadi nilai 2a – b = 2 . 8 – (-2) = 16 + 2 = 18. Soal ini jawabannya A.
Soal 13 – Misalkan A'(-1 ; -2) dan B’ (3 ; 7) adalah hasil bayangan titik A(-1 ; 0) dan B(2 ; 1) oleh transformasi matriks X berordo 2 x 2. Jika C'(0 ; 1) adalah bayangan titik C oleh transformasi tersebut, titik C adalah…
A. (-1 ; 1)
B. (1 ; 1)
C. (1 ; 3)
D. (2 ; -3)
E. (2 ; 3)
Pembahasan
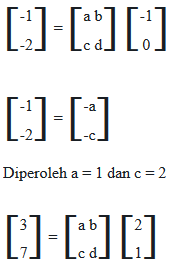
2a + b = 3 atau 2 . 1 + b = 3 maka b = 3 – 2 = 1
2c + d = 7 atau 2 . 2 + d = 7 maak d = 7 – 4 = 3
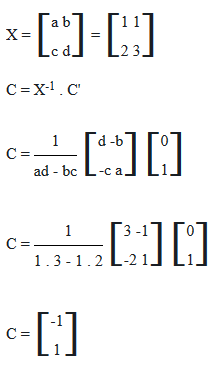
Soal ini jawabannya A.
Soal 14 – Diketahui f(x) = 2x2 – 3x – 5.
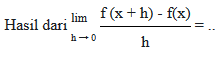
A. 2x – 3
B. 4x – 3
C. 6x – 3
D. 4x3 – 3x2
E. 4x3 – 2x
Pembahasan
f'(x) = 2 . 2 x2 – 1 – 3 . 1 . x1 – 1 – 0
f'(x) = 4x – 3
Soal ini jawabannya B.
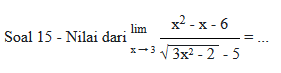
A. 0
B. 25/9
C. 25/6
D. 25/3
E. ∼
Pembahasan

Subtitusi x = 3 sehingga didapat:

Soal ini jawabannya B.
Selanjutnya:
- Pembahasan soal UN matematika IPA 2019 nomor 16 – 30
- Pembahasan soal UN matematika IPA 2019 nomor 31 – 40