Postingan ini membahas contoh soal hukum Kepler yang disertai pembahasannya atau penyelesaiannya + jawaban. Lalu apa itu hukum Kepler ?. Johanes Kepler (1571 – 1630) telah berhasil menjelaskan secara rinci mengenai gerak planet disekitar matahari. Kepler mengemukakan 3 hukum yang berhubungan dengan peredaran planet terhadap matahari yang disebut dengan hukum 1 Kepler, hukum 2 Kepler dan hukum 3 Kepler.
Hukum 1 Kepler menyatakan “Setiap planet bergerak mengitari matahari dengan lintarasan berbentuk elips, matahari berada pada salah satu titik fokusnya“.
Hukum 2 Kepler berbunyi “Suatu garis khayal yang menghubungkan matahari dengan planet menyapu daerah yang luasnya sama dalam selang waktu yang sama“. Hukum 1 dan 2 Kepler jika digambarkan sebagai berikut.
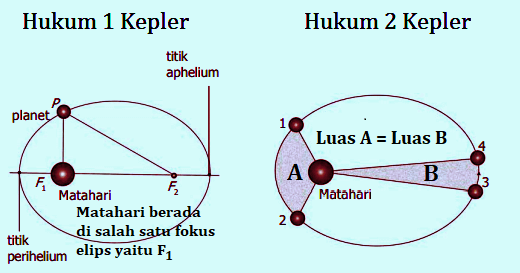
Dan hukum 3 Kepler menyatakan “Perbandingan kuadrat periode planet mengitari matahari terhadap pangkat tiga jarak rata-rata planet ke matahari adalah sama untuk semua planet“. Secara matematis hukum 3 Kepler dirumuskan sebagai berikut.

Keterangan:
- T = periode planet
- R = jarak rata-rata planet ke matahari
- C = konstanta
Contoh soal hukum Kepler
Contoh soal 1
Dua planet A dan B mengorbit matahari. Perbandingan antara jarak planet A dengan planet B ke matahari RA : RB = 1 : 4. Apabila periode planet A mengelilingi matahari adalah 88 hari maka periode planet B adalah…
A. 500 hari
B. 704 hari
C. 724 hari
D. 825 hari
E. 850 hari
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- RA : RB = 1 : 4
- TA = 88 hari
Dengan menggunakan hukum 3 Kepler diperoleh hasil sebagai berikut.
→→
→ TB2 = (88 hari)2 . 64
→ TB = √
→ TB = 88 hari . 8 = 704 hari.
Soal ini jawabannya B.
Contoh soal 2
Planet A dan B masing-masing berjarak rata-rata sebesar P dan Q terhadap matahari. Planet A mengitari matahari dengan periode T. Jika P = 4Q, maka planet B mengitari matahari dengan periode…
A. 1/12 T
B. 1/10 T
C. 1/8 T
D. 1/6 T
E. 1/4 T
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- RA = P = 4Q
- RB = Q
- TA = T
Dengan menggunakan hukum 3 Kepler diperoleh hasil sebagai berikut.
→→
→ TB2 =
→ TB = √
→ TB = 1/8 T.
Soal ini jawabannya C.
Contoh soal 3
Dua planet A dan B mengorbit matahari. Perbandingan antara periode revolusi planet A dan B mengitari matahari adalah 8 : 1. Apabila jarak planet B ke matahari 1,5 SA (SA = satuan astronomi) maka jarak planet A ke matahari adalah…
A. 3,0 SA
B. 4,5 SA
C. 5,0 SA
D. 5,6 SA
E. 6,0 SA
Pembahasan / penyelesaian soal
Dengan menggunakan hukum 3 Kepler diperoleh hasil sebagai berikut.
→→
→ RA3 = (1,5 SA)3 . 64 = (1,5 SA)3 . 43
→ RA = 3√
Soal ini jawabannya E.
Contoh soal 4
Jarak Bumi Matahari = 1 SA sedangkan jarak Mars Matahari 1,6 SA. Bila periode revolusi bumi adalah T, maka periode revolusi Mars adalah…
A. 4T
B. 3T
C. 2T
D. 1,6T
E. 1,2T
Pembahasan / penyelesaian soal
Cara menjawab soal ini sebagai berikut:
→→
→ Tmars2 = 4,096 . T2
→ Tmars = √
→ Tmars mendekati = 2T
Soal ini jawabannya C.
Contoh soal 5
Data fisis planet A, planet B, dan planet Bumi terhadap matahari terlihat seperti tabel dibawah ini.
| Planet A | Bumi | Planet B | |
| Massa | 0,5 M | M | 2,0 M |
| Jarak | 0,5 R | R | 1,5 R |
| Periode | … | 1 tahun | … |
Perbandingan periode planet A dan B adalah…
A. √ 1/27
B. √ 1/3
C. 1/3
D. 1/9
E. 1/27
Pembahasan / penyelesaian soal
Menentukan periode planet A:→
→
→ TA2 =
→ TA = = √ 0,125 tahun
Menentukan periode planet B:
→
→
→ TB2 =
→ TB = √ 3,375 tahun.
Perbandingan periode planet A dan B:
→
Soal ini jawabannya A.