25 Contoh soal eksponen + penyelesaiannya / pembahasan

Contoh soal eksponen nomor 1

Sederhanakanlah.
a. 2x³ . x^-5
b. (4x³y^-2) (3x²y^-10)
c. (-4x²y⁶)^1/3

Penyelesaian soal / pembahasan

2x³ . x^-5 = 2x^{3 – 5} = 2x^-2.
(4x³y^-2) (3x²y^-10) = 4 . 3 . x³ . x² . y^-2 . y^-10 = 12 . x^{3 + 2} . y^{-2 -10} = 12x⁵y^-12.
(-4x²y⁶)^1/3 = (-2²)^1/3 . x^{2 . 1/3} . y^{6 . 1/3} = (-2)^2/3x^2/3y² = (-2x)^2/3y².

Contoh soal eksponen nomor 2

Sederhanakanlah.
a. (2m^-4)^1/2
b. ( $\frac {2} {3}$ m²)³
c. ( $\sqrt {4x}$ )⁵
d. (a⁵ . b³)

Penyelesaian soal / pembahasan

(2m^-4)1/2 = 2^1/2 . m^1/2 . (m^-4)^1/2 = $\sqrt {2}$ m^1/2 . m^-2 = $\sqrt {2}$ m^{1/2 – 2} = m^-3/2 $\sqrt {2}$ .
( $\frac {2} {3}$ m²)³ = ( $\frac {2} {3}$ )³ . m^{2 . 3} = $\frac {2^3} {3^3}$ m⁶ = $\frac {8} {27}$ m⁶.
( $\sqrt {4x}$ )⁵ = ((4x)^1/2)⁵ = (4^1/2 . x^1/2)⁵ = (2 . x^1/2)⁵ = 2⁵ . x^{1/2 . 5} = 32x^5/2.
(a⁵ . b³)^1/5 = a^{5 . 1/5} . b^{3 . 1/5} = ab^3/5.

Contoh soal eksponen nomor 3

Sederhanakanlah.
a. $\frac {4a^5} {2a^{-3}}$
b. $\frac {x^{7}10y^5} {9x^{-3}y^{-2}}$
c. $\left ( \frac{3k^2}{5l^3} \right )^{1/6}$
d. $\left ( \sqrt {\frac{2x^2}{y^4}} \right )^5$

Penyelesaian soal / pembahasan

a. $\frac {4a^5} {2a^{-3}}$ = $\frac {4} {2}$ . a⁵ . a³ = 2 . a^{5 + 3} = 2a⁸.

b. $\frac {x^{7}10y^5} {9x^{-3}y^{-2}}$ = $\frac {10} {9}$ . x⁷ . x³ . y⁵ . y² = $\frac {10} {9}$ . x^{7 + 3} . y^{5 + 2} = $\frac {10} {9}$ x¹⁰y⁷.

c. $\left ( \frac{3k^2}{5l^3} \right )^{1/6}$ = ( $\frac {3} {5}$ . k² . l^-3)^1/6 = ( $\frac {3} {5}$ )^1/6 . k^{2 . 1/6} . l^{-3 . 1/6} = ( $\frac {3} {5}$ )^1/6k^1/3l^-1/2.

d. $\left ( \sqrt {\frac{2x^2}{y^4}} \right )^5$ = ((2x² . y^-4)^1/2)⁵ = (2^1/2 . (x²)^1/2 . (y^-4)^1/2)⁵ = (2^1/2 . x . y^-2)5 = 2^5/2x⁵y^-10.

Contoh soal eksponen nomor 4

Bentuk sederhana dari 4a⁵ x 16a adalah …
A. 8a²
B. 64a⁶
C. 3a⁵
D. 16a⁵

Penyelesaian soal / pembahasan

4a⁵ x 16a = (4 x 16) a^{5 + 1}
= 64a⁶

Soal ini jawabannya B.

Contoh soal eksponen nomor 5

Hasil dari 4p³ q² x 6p² r³ adalah …
A. 10 p⁵ q² r³
B. 24 p⁵ q² r³
C. 24 p⁶ q² r
D. 24 p⁶ q² r³

Penyelesaian soal / pembahasan

4p³ q² x 6 p² r³
= (4 x6) p^{3 + 2} q² r³
= 24 p⁵ q² r³

Soal ini jawabannya B.

Contoh soal eksponen nomor 6

Hasil dari 125^2/3 adalah …
A. 5
B. 15
C. 25
D. 50

Penyelesaian soal / pembahasan

125^2/3 = (5³)^2/3
= 5^{3 x 2/3} = 5²
= 25

Soal ini jawabannya C.

Contoh soal eksponen nomor 7

∛ 343 = …
A. 7
B. 6
C. -6
D. -7

Penyelesaian soal / pembahasan

∛ 343 = 343^1/3
= (7³)^1/3
= 7^{3 x 1/3} = 7

Soal ini jawabannya A.

Contoh soal eksponen nomor 8

√ 125 = …
A. 5^2/3
B. 3^5/2
C. 5^3/2
D. 3^2/5

Penyelesaian soal / pembahasan

√ 125 = 125^1/2
= (5³)^1/2
= 5^{3 x 1/2} = 5^3/2

Soal ini jawabannya C.

Contoh soal eksponen nomor 9

Bentuk dari 3^2/3 sama dengan …
A. $\sqrt [3] {3^2}$
B. $\sqrt [3] {3}$
C. $\sqrt {3^2}$
D. $\sqrt {3}$

Penyelesaian soal / Pembahasan

3^2/3 = $\sqrt [3] {3^2}$ . Soal ini jawabannya A.

Contoh soal eksponen nomor 10

2³ + 2⁵ = …
A. 2⁵
B. 2⁸
C. 5 x 2³
D. 3 x 2³

Penyelesaian soal / pembahasan

2³ + 2⁵ = 2³ + (2² x 2³)
= 2³ + (4 x 2³)
= (1 + 4) x 2³
= 5 x 2³

Soal ini jawabannya C.

Contoh soal eksponen nomor 11

Diketahui x ≠ 0 dan y ≠ 0, bentuk sederhana dari (

2x-5 y3

8x3 y-2

)2 adalah …
A.

y¹⁰

4 x¹⁶

y²

4 x⁴

y¹⁰

16 x¹⁶

y²

16 x⁴

16 y¹⁰

x¹⁶

Penyelesaian soal / pembahasan

Untuk menjawab soal ini kita satukan setiap variabel x atau y menjadi satu pembilang atau penyebut dengan cara berikut ini.

→ (

2y3 y2

8x3 x5

)2
→ (

y3 + 2

4x3 + 5

)2
→ (

4x8

)2
→

y5 . 2

42 x(8 . 2)

→

y10

16x16

Soal ini jawabannya C. Pada jawaban diatas, kita memindahkan ruas variabel dengan pangkat negatif. Ini bertujuan agar hasil yang diperoleh pangkatnya positif.

Contoh soal eksponen nomor 12

Bentuk sederhana dari (

5p-2 q2

25p3 q4

)-1 adalah …
A. 25p5 q2
B. 5 p5 q2
C. p5 q2
D. 1/5 p5 q2
E. 1/25 p5 q2

Penyelesaian soal / pembahasan

Untuk menjawab soal ini kita satu ruaskan p dengan p dan q dengan q sehingga diperoleh hasil sebagai berikut:

→ (

p-2 p-3

5q4 q-2

)-1
→ (

p-2 – 3

5q4 – 2

)-1
→ (

p-5

5q2

)-1
→

5q-2

→

p5 q2

Soal ini jawabannya D. Pada jawaban soal diatas, pangkat -1 kita hilangkan dengan cara mengganti tanda pangkat pada p dan q negatif menjadi positif dan sebaliknya. Jadi bentuk sederhana soal diataa adalah 1/5 p5q2.

Contoh soal eksponen nomor 13

Bentuk sederhana dari (

a-2 b1/2

b-1/2 (a b)

)2 adalah ..
A.

a²

b²

a⁶

a⁶ b

Penyelesaian soal / pembahasan

Langkah-langkah menjawab soal ini sebagai berikut:

→ (

a-2

)2
→

a(-2 . 2) b2

(ab)2

→

a-4 b2

a2 b2

→

a2 a4

→

Soal ini jawabannya D.

Contoh soal eksponen nomor 14

Tentukan bentuk lain dari

m-1

(m-1 – 1)

Penyelesaian soal / pembahasan

Langkah-langkah menjawab soal ini sebagai berikut:

→

1/m

1/m – 1

→

m (1/m – 1)

→

1 – m

Contoh soal eksponen nomor 15

Tentukan bentuk sederhana dari (

a1/2 b-3

a-1 b-3/2

)2/3

Penyelesaian soal / pembahasan

Untuk menjawab soal ini kita kalikan semua pangkat dengan 2/3 sehingga didapat:

→

a1/3 b-2

a-2/3 b-1

→ a1/3 a2/3 b-2 b1 = a . b-1 =

Contoh soal eksponen nomor 16

Penyelesaian dari 5-2x + 2 + 74 . 5-x – 3 ≥ 0 adalah…
A. x ≤ 3 atau x ≥ 1/25
B. -3 ≤ x ≤ 1/25
C. x ≤ 2
D. x ≥ 2
E. x ≥ -2

Penyelesaian soal / pembahasan

Pertidaksamaan eksponen diatas diubah bentuknya menjadi seperti dibawah ini:
5-2x . 52 + 74 . 5-x – 3 ≥ 0
25 . 5-2x + 74 . 5-x – 3 ≥ 0
Misalkan p = 5-x maka pertidaksamaan menjadi:
25p2 + 74p – 3 ≥ 0
(25p – 1) (p + 3) ≥ 0
p1 = 1/25 atau p2 = -3
p = -3 tidak mungkin jadi nilai p yang tepat adalah p = 1/25.
5-x ≥ 1/25 atau 5-x ≥ 5-2
-x ≥ -2 atau x ≤ 2

Soal ini jawabannya C.

Contoh soal eksponen nomor 17

Nilai x yang memenuhi pertidaksamaan 3 . 4x – 7 . 2x + 2 > 0 adalah…
A. x < -1 atau x > 2log 3
B. x < 2log 1/3 atau x > 1
C. 2log 3 < x < 1
D. x < 1 atau x > 2log 1/3
E. 1 < x < 2log 1/3

Penyelesaian soal / pembahasan

Pertidaksamaan eksponen diatas diubah bentuknya menjadi seperti dibawah ini:
3 . 22x – 7 . 2x + 2 > 0
Misalkan p = 2x maka pertidaksamaan menjadi:
3p2 – 7p + 2 >0
(3p – 1) (p – 2) > 0
p = 1/3 atau p = 2
2x = 1/3 maka x = 2log 1/3
2x = 2 maka x = 1
Karena notasi pertidaksamaan lebih dari (>) maka penyelesaian yang tepat adalah x < 2log 1/3 atau x > 1. Soal ini jawabannya B.

Contoh soal eksponen nomor 18

Nilai x yang memenuhi b2x + 10 < 7 . bx dengan b > 1 adalah…
A. x < blog 2
B. x > blog 5
C. x < b log 2 atau x > blog 5
D. blog 2 < x < blog 5
E. x > blog 2

Penyelesaian soal / pembahasan

Pertidaksamaan diata diubah bentuknya menjadi: b2x – 7 . bx + 10 < 0
Misalkan p = bx maka pertidaksamaan menjadi:
p2 – 7p + 10 < 0
(p – 2) (p – 5) < 0
p = 2 atau p = 5
bx = 2 maka x = blog 2
bx = 5 maka x = blog 5
Karena notasi pertidaksamaan kurang dari (<) maka nilai x yang memenuhi blog 2 < x < blog 5
Soal ini jawabannya D.

Contoh soal eksponen nomor 19

Tentukan nilai x yang memenuhi persamaan 5x + 1 = 253x – 4.

Penyelesaian soal / pembahasan

Cara menjawab soal ini sebagai berikut:
5x + 1 = 253x – 4
5x + 1 = 52 (3x – 4)
5x + 1 = 56x – 8
x + 1 = 6x – 8 atau 6x – x = 1 + 9
5x = 10
x = 10/5 = 2

Contoh soal eksponen nomor 20

Tentukan nilai x yang memenuhi persamaan 42x + 3 = 1/64.

Penyelesaian soal / pembahasan

42x + 3 =

42x + 3 = 4-3
2x + 3 = -3 atau 2x = 3 + 3 = 6
x =

= 3

Contoh soal eksponen nomor 21

Tentukan penyelesaian dari persamaan √

32x + 1

= 9x – 2

Penyelesaian soal / pembahasan

(32x + 1)1/2 = 32 (x – 2)
3x + 1/2 = 32x – 4
x +

= 2x – 4
2x – x =

+ 4
x =

= 4

Contoh soal eksponen nomor 22

Tentukan nilai x yang memenuhi persamaan 4x = 2x + 1 + 3

Penyelesaian / pembahasan

Soal diatas diubah bentuknya menjadi (2x)2 = 2x . 2 + 3 atau (2x)2 – 2x . 2 – 3 = 0.
Misal p = 2x maka persamaan menjadi:
p2 – 2p – 3 = 0
(p + 1) (p – 3) = 0
p = – 1 atau p = 3
p = -1 (tidak mungkin) jadi p = 3.
3 = 2x
log 3 = log 2x = x log 2
Jadi nilai yang memenuhi adalah x = 2log 3.

Contoh soal eksponen nomor 23

Jika 2 . 4x + 23 – 2x = 17 maka tentukan nilai dari 22x

Penyelesaian soal / pembahasan

Ubah terlebih dahulu bentuk persamaan menjadi seperti dibawah ini:
2 . 22x + 23 . 2-2x – 17 = 0 (dikali 22x)
2 . 22x . 22x + 8 . 2-2x . 22x – 17 . 22x = 0 atau 2 . 2(2x)2 – 17 . 22x + 8 = 0
Misalkan p = 22x maka persamaan menjadi:
2p2 – 17p + 8 = 0
(2p – 1) (p – 8) = 0
p = 1/2 atau p = 8
Jadi nilai 22x yang memenuhi adalah 1/2 atau 8.

Contoh soal eksponen nomor 24

Tentukan jumlah akar-akar dari persamaan 5x + 1 + 51 – x = 11.

Penyelesaian / pembahasan

Persamaan diatas diubah bentuknya menjadi:
5 . 5x + 5 . 5-x – 11 = 0 (dikali 5x)
5 . 5x . 5x + 5 . 5-x . 5x – 11 . 5x = 0
5 . 52x – 11 . 5x + 5 = 0
Misalkan p = 5x maka persamaan menjadi:
5p2 – 11p + 5 = 0
a = 5, b = – 11 dan c = 5
p1 . p2 = c/a = 5/5 = 1
5x1 . 5x2 = 1
5x1 + x2 = 50
x1 + x2 = 0.
Jadi jumlah akar-akar persamaan diatas = 0.

Contoh soal eksponen nomor 25

Jika x1 dan x2 adalah akar-akar persamaan 2 . 92x – 1 – 5 . 32x + 18 = 0 maka hitunglah x1 + x2

Penyelesaian soal / pembahasan

Persamaan diatas diubah bentuknya menjadi seperti dibawah ini:
2 . 32 (2x -1) – 5 . 32x + 18 = 0
2 . 3(2x)2 . 3-2 – 5 . 32x + 18 = 0 (dikali 32 atau 9)
2 . 3(2x)2 – 45 . 32x + 162 = 0
Misalkan p = 32x maka persamaan menjadi:
2p2 – 45p + 162 = 0
a = 2, b = -45 dan c = 162
p1 . p2 = c/a = 162/2 = 81
32x1 . 32x2 = 81
32 (x1 + x2) = 34
2 (x1 + x2) = 4 atau x1 + x2 = 4/2 = 2.

Contoh soal eksponen kurikulum merdeka

Contoh soal eksponen kurikulum merdeka 1

Sederhanakanlah.
a. $\left ( \frac{2^{4} x 3^6 }{2^{3} x 3^{2}} \right )^{3}$
b. (3u³v⁵) (9u⁴v)
c. $\left ( \frac{n^{-1} x r^4 }{5n^{-6} x r^{4}} \right )^{2}$

Pembahasan

a. (2^{4 – 3} x 3^{6 – 2})³ = (2 x 3⁴)³ = 2³ x 3^{4 x 3}= 2³ x 3¹²
b. (3 x 9) u^{3 + 4} v^{5 + 1} = 27u⁷v⁶
c. $\frac {n^{-1 + 6}} {5}$ = $\frac {n^5} {5}$

Contoh soal eksponen kurikulum merdeka 2

Bakteri E.coli menyebabkan penyakit diare pada manusia. Seorang peneliti mengamati pertumbuhan 50 bakteri ini pada sepotong makanan dan menemukan bahwa bakteri ini membelah menjadi 2 setiap seperempat jam.

Gambarkan tabel dan grafik yang menunjukkan pertumbuhan bakteri ini dari fase 0 sampai fase 5.
Modelkan fungsi yang menggambarkan pertumbuhan bakteri E.coli setiap seperempat jam.
Prediksi berapa banyak bakteri setelah 3 dan 4 jam pertama.

Pembahasan

Jawaban soal 1

Tabel pertumbuhan bakteri.

Fase	Banyak bakteri
0	50
1	100
2	200
3	400
4	800
5	1.600

Grafik pertumbuhan bakteri sebagai berikut.

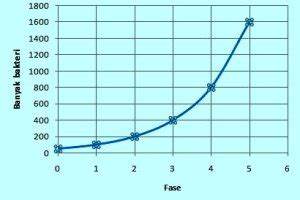
Jawaban soal 2

Model fungsi = f(x) = 50 (2)^x dengan x = 0, 1, 2, 3, …

Jawaban soal 3

3 jam = $\frac {1} {4}$ x 12 jam (x = 12)
f(12) = 50 (2)¹² = 204.800
4 jam = $\frac {1} {6}$ x 16 jama (x = 16)
f(16) = 50 . (2)¹⁶ = 3.276.800

Contoh soal eksponen kurikulum merdeka 3

Pada tahun 2015 kasus positif HIV-AIDS berjumlah sekitar 36 juta jiwa. Jumlah ini meningkat 2% setiap tahun dari tahun 2010 hingga 2015. Jika peningkatan kasus positif HIV di tahun-tahun berikutnya diprediksi bertambah secara eksponen pada peningkatan 2% setiap tahun, berapa banyak kasus yang terjadi pada tahun 2020?

Pembahasan

Peningkatan kasus (%) = 100% + 2% = 102% = 1,02
f(x) = 36 juta (1,02)^x
2020 – 2015 = 5 (x = 5)
f(5) = 36 juta (1,02)⁵
f(5) = 36 juta . (1,1)
f(5) = 39.600.000

Contoh soal eksponen kurikulum merdeka 4

Dua ratus mg zat disuntikkan ke dalam tubuh pasien yang menderita penyakit kanker paru-paru. Zat tersebut akan dikeluarkan dari dalam tubuh melalui ginjal setiap 1 jam. Jika setiap 1 jam 50% zat tersebut dikeluarkan dari dalam tubuh pasien, berapa mg zat tersebut yang masih tersisa di dalam tubuh pasien setelah 5 jam.

Pembahasan

f(x) = 200 mg . $\left ( \frac{1}{2} \right )^{x}$
f(5) = 200 mg . $\left ( \frac{1}{2} \right )^{5}$
f(5) = $\frac {200} {2^5}$ mg = $\frac {200} {32}$ mg = 6,25

Contoh soal eksponen kurikulum merdeka 5

Massa suatu zat radioaktif adalah 0,3 kg pada pukul 10 pagi. Tingkat peluruhan zat radioaktif tersebut adalah 15% setiap jam. Berapakah jumlah zat radioaktif tersebut 8 jam kemudian?

Pembahasan

Jumlah zat radioaktif (%) = 100% – 15% = 85% = 0,85
f(x) 0,3 kg . (0,85)x
f(8) = 0,3 kg . (0,85)8 = 0,08 kg

Contoh soal eksponen kurikulum merdeka 6

Sebuah bola basket dijatuhkan dari ketinggian 6 meter. Bola tersebut menyentuh tanah dan kemudian melambung kembali setinggi $\frac {3} {5}$ dari tinggi sebelumnya. Bola tersebut terpantul dan melambung kembali dengan ketinggian yang sama sampai akhirnya benar-benar berhenti melambung dan jatuh ke tanah.

Gambarkan grafik fungsi perubahan ketinggian lambungan bola hingga akhirnya menyentuh tanah.
Pada lambungan ke berapa, bola akhirnya berhenti melambung?

Pembahasan

Berdasarkan grafik di atas, bola basket berhenti melambung pada pantulan ke 9 atau ke 10 karena mendekati 0.

Contoh soal eksponen kurikulum merdeka 7

Selesaikanlah.
a. $\left ( \frac{3a^{-2} b}{a^{2}b^{2}c^{-1}} \right )^{-3}$
b. $\sqrt[3]{\frac{24x^{2}y^5}{3x^{5}y^{11}}}$

Pembahasan

Jawaban a.

$\left ( \frac{3c}{a^{2 + 2}b^{5 - 1}} \right )^{-3}$ = $\left ( \frac{3c}{a^{4}b^{4}} \right )^{-3}$
= $\frac{a^{4 x 3}b^{4 x 3}}{3^{3}c^3}$ = $\frac{a^{12}b^{12}}{27c^3}$

Jawaban b

$\left ( \frac{24x^{2}y^5}{3x^{5}y^{11}} \right )^{\frac{1}{3}}$ = $\left ( \frac{8}{x^{5 - 2}y^{11 - 5}} \right )^{\frac{1}{3}}$
= $\left ( \frac{2^3}{x^{3}y^{6}} \right )^{\frac{1}{3}}$ = $\frac {2^{3x1/3}} {x^{3x1/3}y^{6x1/3}}$ = $\frac {2} {xy^2}$

Contoh soal eksponen kurikulum merdeka 8

Pembahasan

Jawaban a.

(x^{-5 – 1} y^{4 – 1})^-2 . (x^{7 + 4} y^{-3 – 6})^-1/2
(x^{-6 . -2} . y^{3 . (-2)}) (x^{11 . (-1/2)} y^{-9 . -1/2})
x¹² . y^-6 . x^-11/2 . y^9/2
x^{12 – 1/2} y^{-6 + 9/2} = x^11/2 y^3/2
= (x¹¹ y³)^1/2

Jawaban b.

m^{10 . 3} . n^{-2 . 3} . m^{5 . 3} . n^{-5 . 3} . m^-1 . n^-1
m³⁰ . n^-6 . m¹⁵ . n^-15 . m^-1 . n^-1
m^{30 + 15 – 1} n^{-6 – 15 – 1} = m⁴⁴ . n^-22
= $\frac {m^{44}} {n^{22}}$

25 Contoh soal eksponen + penyelesaiannya / pembahasan

Contoh soal eksponen kurikulum merdeka

Tinggalkan Balasan Batalkan balasan