Pembahasan soal UTBK 2020 TPS Kuantitatif + jawaban

Dibawah ini adalah pembahasan soal-soal UTBK tahun 2020 TPS tentang pengetahuan kuantitatif. Pengetahuan kuatitatif berkaitan dengan matematika dan perhitungan. Soal UTBK 2020 sebanyak 20 soal dan dipilih secara random. Pembahasan soal UTBK 2020 ini dapat dijadikan bahan belajar untuk menghadapi UTBK 2021, yang akan dimulai pada tanggal 12 – 18 April 2021 untuk gelombang pertama dan 26 April – 2 Mei 2021 untuk gelombang kedua.

Soal UTBK 1

Diantara bilangan berikut, manakah yang nilainya lebih besar dari x 20%.
A. x 24%
B. x 33%
C. x 90%
D. x 30%
E. x 42%

Pembahasan

20% : 3 = 6,67 %. Nilai yang lebih besar dari 6,67 % adalah 30% : 4 = 7,5 %. Soal ini jawabannya D.

---

Soal UTBK 2

Jika f²(x) = 2f(x) + 5 memiliki akar-akar x₁ dan x₂ dengan f(x) = 1 – 2x maka jumlah akar-akar persamaan tersebut adalah …
A. 1/2
B. 0
C. 2
D. 3
E. 4

Pembahasan

• f²(x) – 2f(x) – 5 = 0
• (1 – 2x)² – 2 (1 – 2x) – 5 = 0
• 1 – 4x + 4x² – 2 + 4x – 5 = 0
• 4x² – 6 = 0
• a = 4, b = 0 dan c = -6
• x₁ + x₂ = – = – = 0

Soal ini jawabannya B.

---

Soal UTBK 3

Perbandingan usia Irzam dengan ayahnya lima tahun lalu 1 : 3. Tahun ini, selisih keduanya 30 tahun. Berapakah usia Irzam dan ayahnya 10 tahun lagi ?.
A. 30 tahun dan 60 tahun
B. 30 tahun dan 55 tahun
C. 25 tahun dan 55 tahun
D. 20 tahun dan 55 tahun
E. 10 tahun dan 40 tahun

Pembahasan

Misalkan usia Irzam = x dan usia ayah = y maka diperoleh hasil sebagai berikut.

→ y – x = 30 atau y = 30 + x
→

x – 5

y – 5

=

1

3

→

x – 5

(30 + x) – 5

=

1

3

→

x – 5

25 + x

=

1

3

→ 25 + x = 3x – 15
→ 25 + 15 = 3x – x = 2x
→ x = 40/2 = 20
→ y = 30 + x = 30 + 20 = 50

Jadi usia Irzam dan usia ayah 10 tahun lagi sebagai berikut.

• usia Irzam (x) = 20 + 10 = 30 tahun
• usia ayah (y) = 50 + 10 = 60 tahun

Soal ini jawabannya A.

---

Soal UTBK 4

Diberikan 5 huruf konsonan q, w, r, t dan y serta huruf vokal a, i dan e. Dari huruf tersebut akan dibuat password yang terdiri atas 5 huruf dengan 3 huruf konsonan dan 2 huruf vokal yang berbeda. Banyaknya password yang terbentuk adalah …
A. 3600
B. 2450
C. 1250
D. 120
E. 90

Pembahasan

Cara menjawab soal ini sebagai berikut.

→ Banyak cara menyusun 3 huruf konsonan dari 5 huruf =

5!

(5 – 3)!

= 60
→ Banyak cara menyusun 2 huruf vokal dari 3 huruf =

3!

(3 – 2)!

= 6
→ Banyak cara menyusun 3 huruf konsonan dan 2 huruf vokal = 10
→ Banyak password = 60 x 6 x 10 = 3600

Soal ini jawabannya A.

---

Soal UTBK 5

Pada gambar dibawah ini diketahui bahwa garis a dan b adalah sejajar. Besar sudut x^o adalah …

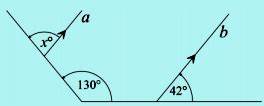
A. 44^o
B. 45^o
C. 55^o
D. 88^o
E. 90^o

Pembahasan

• x^o = (180 – 42) – 50
• x^o = 138 – 50 = 88^o

Soal ini jawabannya D.

---

Soal UTBK 6

Pada gambar dibawah, AB dan BC adalah garis singgung. Panjang OB = 25 cm dan OA = 7 cm. Luas layang-layang OABC adalah…
A. 168 cm2
B. 82 cm2
C. 60 cm2
D. 32 cm2
E. 4 cm2

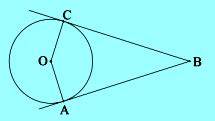
Pembahasan

Luas layang-layang = 2 x 1/2 x OA x AB
AB = √

OB² – OA²

AB = √

(25 cm)² – (7 cm)²

= √

576 cm²

= 24 cm
Luas layang-layang = 2 x 1/2 x 7 cm x 24 cm = 168 cm²

Soal ini jawabannya A.

---

Soal UTBK 7

lim

x → 1

x¹⁰⁰ – 1

x² – 1

= …
A. 0
B. 1
C. 50
D. 100
E. ∞

Pembahasan

Misal f(x) = x¹⁰⁰ – 1 maka f'(x) = 100x⁹⁹ dan g(x) = x² – 1 maka g'(x) = 2x. Dengan menggunakan aturan L’hospital diperoleh hasil sebagai berikut.

→

lim

x → 1

f(x)

g(x)

=

lim

x → 1

f'(x)

g'(x)

→

lim

x → 1

x¹⁰⁰ – 1

x² – 1

=

lim

x → 1

100 x⁹⁹

2x

→

lim

x → 1

100 1⁹⁹

2 . 1

= 50

Soal ini jawabannya C.

---

Soal UTBK 8

Dari 4 huruf a, b, c, d dan 5 angka 2, 3, 4, 5, 6 akan disusun sebuah password yang terdiri dari satu huruf dan 3 angka. Jika digit-digit password tersebut tidak boleh berulang, maka banyaknya password yang dapat dibentuk adalah …
A. 40
B. 480
C. 800
D. 960
E. 1.200

Pembahasan

Cara menjawab soal ini sebagai berikut.

→

5!

(5 – 3) !

x 4 x 4
→

5 x 4 x 3 x 2!

2!

x 8 = 960

Soal ini jawabannya D.

---

Soal UTBK 9

Perbandingan kecepatan A dan B dalam mengcopy pada mesin fotocopy adalah 4 : 6. Jika A dapat menghasilkan 360 lembar dalam 8 menit, berapakah waktu yang dibutuhkan B untuk menghasilkan 5400 lembar kertas?.
A. 0,5 jam
B. 1 jam
C. 1 jam 10 menit
D. 1 jam 20 menit
E. 1 jam 30 menit

Pembahasan

→

v_A

v_B

=

(lembar / t)_A

(lembar / t)_B

→

4

6

=

360 / 8 menit

5400 / t_B

→

2

3

=

45 / menit

5400 / t_B

→ t_B =

2 . 5400

3 . 45

menit = 80 menit = 1 jam 20 menit

Soal ini jawabannya D.

---

Soal UTBK 10

Diketahui matriks M = . Jika det M = 24, maka nilai dari x adalah …
A. 1
B. 2
C. 3
D. 4
E. 5

Pembahasan

• Det M = 24
• a . d – b . c = 24
• (4 – 2x) . 1 – (-4) . 7 = 24
• 4 – 2x + 28 = 24
• 2x = 4 + 28 – 24 = 8
• x = 8/2 = 4

Soal ini jawabannya D.

---

Soal UTBK 11

Diketahui matriks A = . Jika matriks A adalah matriks singular, maka nilai x = …
A. -3
B. -2
C. -1
D. 2
E. 3

Pembahasan

Matriks singular adalah matriks dengan determinan det = 0.

• Det A = 0
• a . d – b . c = 0
• – 3 . – 4 – 4 (x + 1) = 0
• 12 = 4x + 4
• 4x = 12 – 4 = 8
• x = 8/4 = 2

Soal ini jawabannya D.

---

Soal UTBK 12

Perhatikan grafik parabola dibawah, manakah pernyataan yang benar?.

1. sumbu simetri x = 1
2. Titik puncak (1, -9)
3. y = x² + 2x – 8
4. Nilai D > 0

A. 1, 2, 3 saja yang benar
B. 1 dan 3 yang benar
C. 2 dan 4 yang benar
D. 4 saja yang benar
E. semua benar

Pembahasan

Tentukan terlebih dahulu persamaan fungsi kuadrat diatas dengan cara dibawah ini.

• y = a (x – x₁) (x – x₂)
• -8 = a (x – (-2)) (x – 4)
• -8 = a (x + 2) (x – 4)
• -8 = a (x² – 2x – 8)
• Subtitusi x = 0
• -8 = a (0² – 2 . 0 – 8)
• a = -8/-8 = 1
• y = x² – 2x – 8 (pernyataan nomor 3 salah)

→ sumbu simetri x = –

b

2a

= –

– 2

2 . 1

= 1 (pernyataan 1 benar)
→ Titik puncak = (1,

b² – 4ac

4a

→ Titik puncak = (1,

(-2)² – 4 . 1 . -8

4 . 1

→ Titik puncak = (1, 9) pernyataan 2 salah.
→ pernyataan 4 benar

Soal ini jawabannya D.

---

Soal UTBK 13

Agar garis (m + 1)x + (2m – 5) y = 8 dan (m – 2)x – 4y = 2 saling tegak lurus, maka m = …
A. 1
B. 2
C. 3
D. 4
E. 5

Pembahasan

Syarat dua garis saling tegak lurus adalah m₁ . m₂ = -1. Dengan menggunakan syarat tersebut diperoleh hasil sebagai berikut.

→ m₁ = –

m + 1

2m – 5

→ m₂ =

m – 2

4

→ m₁ . m₂ = – 1
→ –

m + 1

2m – 5

x

m – 2

4

= -1
→ m² – m – 2 = 8m – 20
→ m² – 9m + 18 = 0
→ (m – 6) (m – 3) = 0
→ m = 6 atau m = 3

Soal ini jawabannya C.

---

Soal UTBK 14

Perhatikan gambar berikut.

Garis l mewakili fungsi f. Berapakah nilai dari f(10) ?.
A. 15
B. 13
C. 12
D. 11
E. 9

Pembahasan

→

y – y₁

y₂ – y₁

=

x – x₁

x₂ – x₁

→

y – 2

0 – 2

=

x – 0

-2 – 0

→

y – 2

– 2

=

x

-2

→ y = x + 2
→ f(x) = x + 2
→ f(10) = 10 + 2 = 12

Soal ini jawabannya C.

---

Soal UTBK 15

Kurva y = x² – 5 dan garis y = 2x + 3 akan berpotongan dititik …
A. (-2, -1)
B. (-2, 4)
C. (-2, 1)
D. (4, 7)
E. (4, 12)

Pembahasan

• x² – 5 = 2x + 3
• x² – 2x – 5 – 3 = 0
• x² – 2x – 8 = 0
• (x – 4) (x + 2) = 0
• x = 4 atau x = – 2
• Subtitusi x = 4 ke y = 2x + 3 = 2 . 4 + 3 = 11 (titik potong pertama [4, 11])
• Subtitusi x = – 2 ke y = 2x + 3 = 2 . – 2 + 3 = -1 (titik potong kedua [-2, -1])

Jadi jawaban yang tepat adalah A.

---

Soal UTBK 16

Diketahui suatu operasi tertentu P(a * b * c * d) = a – d + 2b + c, maka nilai dari P(3 * (-2) * 1 * 4) = …
A. – 10
B. – 8
C. – 4
D. 5
E. 6

Pembahasan

Diketahui a = 3, b = -2, c = 1 dan d = 4 maka diperoleh hasil P(3 * (-2) * 1 * 4) = 3 – 4 + 2 . (-2) + 1 = – 4. Soal ini jawabannya C.

---

Soal UTBK 17

Diberikan fungsi f dan g dengan g(x) = f(x² + 2). Jika diketahui bahwa g'(1) = 8 maka f'(3) = ….
A. 6
B. 5
C. 4
D. 3
E. 2

Pembahasan

Misalkan U = x² + 2 maka U’ = 2x. Dengan menggunakan aturan rantai turunan g'(x) = f'(U) . U’ diperoleh hasil sebagai berikut.

• g(x) = f(U)
• g'(x) = f'(U) . U’
• g'(x) = f'(x² + 2) . 2x
• subtitusi x = 1
• g'(1) = f'(1² + 2) . 2 . 1
• 8 = f'(3) . 2
• f'(3) = 8/2 = 4

Soal ini jawabannya C.

---

Soal UTBK 18

Diketahui f(x) = 2x – 1 dan (g o f)(x) = 3x² – 5x + 2. Nilai g(1) = …
A. -2
B. 0
C. 1
D. 2
E. 3

Pembahasan

• (g o f) (x) = 3x² – 5x + 2
• g (2x – 1) = 3x² – 5x + 2
• Subtitusi x = 1
• g (2 . 1 – 1) = 3 . 1² – 5 . 1 + 2
• g(1) = 0

Soal ini jawabannya B.

---

Soal UTBK 19

Jika f(x²) + 2 f(x) = 1 dan f(x) = 3x + 5 maka nilai x₁ + x₂ adalah ….
A. -2
B. -1
C. 0
D. 1
E. 2

Pembahasan

• f(x²) + 2 f(x) – 1 = 0
• 3x² + 5 + 2 (3x + 5) – 1 = 0
• 3x² + 5 – 6x + 10 – 1 = 0
• 3x² – 6x + 14 = 0

a = 3, b = -6 dan c = 14. Maka x₁ + x₂ = – = – = 2. Soal ini jawabannya E.

---

Soal UTBK 20

Diketahui suatu barisan dengan a₁ = 5 dan a₂ = 7. Jika a_n+1 = a_n+2 – 3a_n maka a₃ + a₂ = …
A. 15
B. 19
C. 22
D. 25
E. 29

Pembahasan

Tentukan a₃ dengan subtitusi n = 1 ke a_n+1 = a_n+2 – 3a_n sehingga diperoleh hasil sebagai berikut.

• a_{1 + 1} = a_{1 + 2} – 3a₁
• a₂ = a₃ – 3a₁
• a₃ = 3a₁ + a₂ = 3 . 5 + 7 = 22

Jadi a₃ + a₂ = 22 + 7 = 29. Soal ini jawabannya E.