Pembahasan soal UNBK matematika IPS nomor 21 – 22 – 23 – 24 – 25 – 26

Postingan ini menyajikan pembahasan soal UNBK matematika IPS tahun 2019. Artikel ini lanjutan dari pembahasan soal UN matematika IPS 2019 nomor 1 – 20. Jadi pembahasan ini dimulai dari nomor 21 hingga nomor 26.

Soal UNBK matematika IPS 2019 nomor 21

Turunan pertama fungsi f(x) = (4x2 – 12 x) (x + 2) adalah…
A. f'(x) = 12x2 – 4x – 24
B. f'(x) = 12x2 – 8x + 24
C. f'(x) = 24x – 8
D. f'(x) = 12x2 – 16x + 24
E. f'(x) = 12x2 – 8x – 24.

Pembahasan

Misalkan U = 4x2 – 12x) maka U’ = 8x – 12
V = x + 2 maka V’ = 1
f'(x) = U’ V + U V’
f'(x) = (8x – 12) (x + 2) + (4x2 – 12x) . 1
f'(x) = 8x2 + 16x – 12x – 24 + 4x2 – 12x
f'(x) = 12x2 – 8x – 24
Jawaban soal ini E.

---

Soal UNBK matematika IPS nomor 22

Grafik fungsi f(x) = x3 + 3/2 x2 – 18x + 5 naik pada interval …
A. -2 < x < 3
B. -3 < x < 2
C. x < 2 atau x > 3
D. x < -3 atau x > 2
E.. x < – 2 atau x > 3

Pembahasan

Syarat fungsi naik f'(x) > 0
f'(x) = 3x2 + 3x – 18 (dibagi 3)
x2 + x – 6 > 0
(x + 3) (x – 2) > 0
x = – 3 atau x = 2

Untuk menentukan interval, buat garis bilangan seperti gambar dibawah ini.

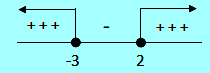
Jadi interval fungsi naik x < -3 atau x > 2. Soal ini jawabannya D.

---

Soal UNBK matematika IPS nomor 23

Hasil dari ∫ (2x3 – 9x2 + 4x – 5) dx = …
A. 1/2 x4 – 6x3 + 2x2 – 5x + c
B. 1/2 x4 – 6x3 + x2 – 5x + c
C. 1/2 x4 – 3x3 + x2 – 5x + c
D. 1/2 x4 – 3x3 + 2x2 – 5x + c
E. 1/2 x4 – 6x3 2 2x2 – 5x + c

Pembahasan

∫ (2x3 – 9x2 + 4x – 5) dx
=

2

3 + 1

x3 + 1 –

9

2 + 1

x2 + 1 +

4

1 + 1

x1 + 1 – 5x + C
=

1

2

x4 – 3x3 + 2x2 – 5x + C

Soal ini jawabannya D.

---

Soal UNBK matematika IPS nomor 24

Diketahui segitiga ABC siku-siku di A dan sin B = 3
7. Nilai tan C adalah…
A. 3/20 √ 10  
B. 7/20 √ 10  
C. 2/3 √ 10  
D. 3/2 √ 10  
E. 7/3 √ 10  

Pembahasan

Pada soal ini diketahui sin B = 3/7 maka panjang AC = 3 dan AB = 7 seperti gambar dibawah (ingat sin = depan / miring)

Selanjutnya kita hitung panjang AB dengan rumus pythagoras dibawah ini:

BC2 = AC2 + AB2
72 = 32 + AB2
AB2 = 49 – 9 = 40
AB = √ 40   = 2 √ 10  

Jadi jawaban soal ini sebagai berikut:

tan C =

depan

samping

tan C =

AB

AC

=

2 √ 10  

3

Soal ini jawabannya C.

---

Soal UNBK matematika IPS nomor 25

Nilai dari cos 300° + sin 150° – tan 135° = …
A. √ 3   – 1
B. √ 3   + 1
C. 0
D. 1
E. 2

Pembahasan

cos 300° + sin 150° – tan 135°
= cos (360 – 60) + sin (180 – 30) – tan (180 – 45)
= cos 60 + sin 30 – tan 45
= 1
2 + 1
2 + 1 = 2
Soal ini jawabannya E.

---

Soal UNBK matematika IPS nomor 26

Periode grafik fungsi f(x) = 2 cos (3
4 x + π)
A. 8/3 π
B. 3/2 π
C. 4/3 π
D. 3/4 π
E. 1/2π

Pembahasan

Pada soal ini diketahui k = 3/4 maka periode fungsi diatas sebagai berikut:

periode =

2π

k

Periode =

2π

3

4

Periode =

8

3

π

Soal ini jawabannya A.