Postingan ini menyajikan pembahasan soal UNBK matematika IPS tahun 2019 nomor 27 hingga 40. Pembahasan soal UNBK matematika IPS ini terdiri dari 2 jenis yaitu pilihan ganda dan soal ISIAN. Soal pilihan ganda dimulai dari nomor 27 hingga 36 sedangkan soal ISIAN dimulai dari nomor 37 hingga 40.
Soal 27 – Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. Jarak titik A ke bidang CDEF sama dengan jarak titik A ke …
A. titik tengah ED
B. titik tengah EF
C. titik pusat CDEF
D. titik E
D. titik D
Pembahasan
Jarak titik A ke bidang CDEF digambarkan sebagai berikut:
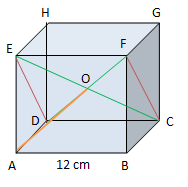
Berdasarkan gambar diatas, jarak titik A ke bidang CDEF adalah sepanjang garis AO, yang sama dengan jarak titik A ke pusat bidang CDEF. Soal ini jawabannya C.
Soal 28 – jika luas bidang diagonal suatu kubus = 36
√ 2
cm2, panjang diagonal ruang kubus adalah…
A. 18
√ 3
cm
B. 15
√ 3
cm
C. 12
√ 3
cm
D. 9
√ 3
cm
E. 6
√ 3
cm
Pembahasan
Luas bidang diagonal kubus = panjang rusuk kubus x panjang diagonal sisi kubus. Jadi jika luas bidang diagonal suatu kubus = 36 √ 2 cm2 maka panjang rusuk kubus = 6 cm dan panjang diagonal sisi kubus = 6 √ 2 cm. Hal ini karena 6 cm x 6 √ 2 cm = 36 √ 2 cm2. Panjang diagonal ruang kubus dihitung dengan rumus pythagoras sebagai berikut:
- (P. diagonal ruang) = (6 cm)2 + (6 √ 2 cm)2
- (P. diagonal ruang) = 36 cm2 + 36 . 2 cm2
- P. diagonal ruang = √ 36 . 3 cm2
- P. diagonal = 6 √ 3 cm
Soal ini jawabannya E.
Soal 29 – Diagram lingkaran berikut menunjukkan banyak warga dalam pemilihan kepala desa di empat daerah.
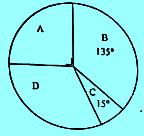
Jika total 1080 warga mengikuti pemilihan tersebut, banyak warga yang memilih di daerah D adalah…
A. 270 warga
B. 300 warga
C. 330 warga
D. 360 warga
E. 390 warga
Pembahasan
Sudut daerah D = 180 – sudut A – sudut B – sudut C
Sudut daerah D = 360 – 90 – 135 – 15 = 120
Warga daerah D = 120/360 x 1080 = 360 warga
Soal ini jawabannya D.
Soal 30 – Tabel berikut menyajikan data nilai ulangan bahasa Indonesia siswa kelas XII.
| Nilai | Frekuensi |
| 40 – 44 | 2 |
| 45 – 49 | 8 |
| 50 – 54 | 15 |
| 55 – 59 | 10 |
| 60 – 64 | 5 |
| 65 – 69 | 10 |
Rata-rata nilai ulangan bahasa Indonesia siswa kelas tersebut adalah…
A. 53,2
B. 55,8
C. 56,3
D. 56,8
E. 58,2
Pembahasan
Jumlah frekuensi soal diatas = 50. Untuk menjawab soal ini tentukan terlebih dahulu titik tengah (xi ), kemudian dikali dengan frekuensi (xi . f)seperti tabel dibawah ini.
| xi | xi . f |
| 42 | 84 |
| 47 | 376 |
| 52 | 780 |
| 57 | 570 |
| 62 | 310 |
| 67 | 670 |
| Jumlah | 2790 |
Jadi nilai rata-rata = 2790 / 50 = 55,8. Soal ini jawabannya B.
Soal 31 – Histogram berikut menyatakan data nilai tes peserta didik kelas XI.
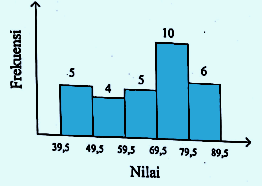
Median dari data tersebut adalah…
A. 70,5
B. 71,2
C. 71,5
D. 75,5
E. 79,5
Pembahasan
Jumlah frekuensi histogram N = 5 + 4 + 5 + 10 + 6 = 30
1/2 N = 15
letak kelas median = histogram ke 4 (frekuensi 10)
fme = 10
TB = 69,5
Σfme = 5 + 4 + 5 = 14
c = 10
Cara menghitung median sebagai berikut:
Me = TB +Me = 69,5 +
Soal ini jawabannya A.
soal 32 – Diketahui data 2, 6, 7, 1, 4. Varians data tersebut adalah…
A. 5,4
B. 5,8
C. 6,0
D. 6,2
E. 6,4
Pembahasan
Nilai rata-rata data = (2 + 6 + 7 + 1 + 4) / 5 = 20 / 5 = 4. Setiap data dikurang nilai rata-rata lalu dikuadratkan sehingga didapat hasil dibawah ini:
(2 – 4)2 = 4
(6 – 4)2 = 4
(7 – 4)2 = 9
(1 – 4)2 = 9
(4 – 4)2 = 0
Jadi varians data tersebut sebagai berikut:
s2 =Jawaban : –
Soal 33 – Dari jumlah siswa yang terdiri dari 3 siswa kelas X, 4 siswa kelas XI dan 5 siswa kelas XII, akan dipilih pengurus OSIS yang terdiri dari ketua, wakil ketua dan sekretaris. Ketua harus berasal dari kelas yang lebih tinggi dari wakil ketua dan sekretaris. Banyak cara memilih pengurus OSIS adalah…
A. 60 cara
B. 105 cara
C. 210 cara
D. 234 cara
E. 1.320 cara
Pembahasan
Jika ketua berasal dari kelas XII (5 siswa) maka wakil dan sekretaris berasal dari kelas XI dan kelas X (jumlah siswa 4 + 3 = 7). Banyak cara kondisi ini sebagai berikut:
P (5, 1) x P (7,2) =P (5, 1) x P (7,2) = 5 x 7 x 6 = 210
Jika ketua berasal dari kelas XI (4 siswa) maka wakil dan sekretasi berasal dari kelas X saja (3 siswa). Banyak cara kondisi ini sebagai berikut:
P (4, 1) x P (3 , 2) =P (4, 1) x P (3 , 2) = 4 x 3 x 2 = 24
Jadi banyak cara memilih pengurus OSIS = 210 + 24 = 234. Soal ini jawabannya C.
Soal 34 – Dalam pemilihan murid untuk lomba tari di suatu sekolah terdapat calon yang terdiri dari 4 orang putri dan 3 orang putra. Jika akan dipilih sepasang murid yang terdiri dari seorang putra dan seorang putri, banyak cara memilih pasangan ada sebanyak…
A. 7 cara
B. 12 cara
C. 21 cara
C. 42 cara
E. 104 cara
Pembahasan
Banyak cara memilih satu putri dari 4 orang = 4
Banyak cara memilih satu putra dari 3 orang = 3
Banyak cara memilih pasangan = 4 x 3 = 12
Soal ini jawabannya B.
Soal 35 – sebuah keranjang berisi 6 bola kuning dan 5 bola hijau. Enam bola diambil sekaligus secara acak. Peluang terambil 4 bola kuning dan 2 bola hijau adalah…
A. 20/77
B. 25/77
C. 30/77
D. 55/77
E. 65/77
Pembahasan
Banyak cara mengambil 4 bola kuning dari 6 bola adalah C (6, 4).
Banyak cara mengambil 2 bola hijau dari 5 bola adalah C (5, 2). Banyak cara mengambil 6 bola dari 11 bola n(S) = C (11, 6).
n(K) =
n(K) = 15 x 10 = 150
n(S) =
n(S) =
P(K) =
Jawaban soal ini B.
Soal 36 – Dua buah dadu dilambungkan secara bersamaan sebanyak 180 kali. Frekuensi harapan muncul mata dadu berjumlah 5 atau 10 adalah…
A. 15 kali
B. 21 kali
C. 25 kali
D. 30 kali
E. 35 kali.
Pembahasan
Misalkan peluang muncul mata dadu berjumlah 5 = P(A) dan peluang muncul mata dadu berjumlah 10 = P(B).
n(A) = (1, 4) ; (2, 3) = 2
n(B) = (1, 9) ; (2, 8) ; (3, 7) ; (4, 6) ; (5, 5) = 5
n(S) = 36
P(A) = n(A) / n(S) = 2 / 36
P(B) = n(B) / n(S) = 5/36
P(A ∪ B) = P(A) + P(B) = 2/36 + 5/36 = 7/36
Frekuensi harapan = 180 . 7/36 = 35 kali
Soal ini jawabannya E.
Soal ISIAN
Soal 37 – Dalam rangka memperingati hari kemerdekaan republik Indonesia, desa X mengadakan perlombaan mengambil kelereng dari wadah dengan aturan sebagai berikut:
- Setiap tim terdiri dari 5 orang dan setiap anggota kelompok harus mengambil kelereng sesuai urutannya.
- Pada pengambilan putaran pertama (5 orang secara bergantian) hanya diperbolehkan mengambil masing-masing satu kelereng.
- Pada putaran ke – n (n > 2), orang pertama setiap kelompok mengambil n kelereng dan selalu bertambah 3 kelereng untuk peserta pada urutan berikutnya dalam kelompok tersebut.
Tim C beranggotakan Aldo, Bambang, Candra, Didi dan Eka (urutan pengambilan kelereng sesuai dengan urutan abjad awal nama). Bersamaan habisnya waktu, ternyata Candra adalah anggota tim C terakhir yang berhasil mengambil 11 kelereng. Banyak kelereng yang berhasil dikumpulkan tim C adalah… kelereng.
Pembahasan
Jumlah kelerang yang terambil:
- Putaran pertama = 1 + 1 + 1 + 1 + 1 = 5
- Putaran kedua = 2 + 5 + 8 + 11 + 14 = 40
- Putaran ketiga = 3 + 6 + 9 + 12 + 15 = 45
- Putaran keempat = 4 + 7 + 10 + 13 + 16 = 50
- Putaran kelima = 5 + 8 + 11 = 24
Jadi jumlah kelereng yang dikumpulkan tim C = 5 + 40 + 45 + 50 + 24 = 164 kelereng.
Soal 39 – Andi berada di titik A dan berjarak 6 √ 3 m dari titik B dengan sudut elevasi dititik A terhadap tiang bendera adalah 60°. Andi akan memasang tali dengan cara merobohkan tiang bendera. Dia harus bergerak menuju titik C sehingga jarak antara ujung tiang bendera ke titik C adalah 2 m seperti gambar berikut.
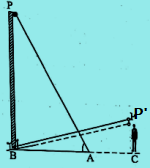
Jika α adalah sudut yang dibentuk BP’ dan BC, nilai dari 1/sin α adalah…
Pembahasan
Berdasarkan segitiga BAP diperoleh:
tan A = BP / BA
BP = tan A . BA = tan 60° . 6 √ 3 = √ 3 . 6 √ 3 = 18 m
Segitiga BCP sebangun dengan segitiga BCP’ sehingga panjang BP = BP’ = 18 m.
sin α = CP’ / BP’ = 2 / 18 = 1 / 9
1 / sin α = 9
Soal 40 – didalam sebuah kantong terdapat 3 dadu berwarna hitam, 2 dadu berwarna cokelat dan 2 dadu berwarna merah. Jika diambil 2 buah dadu secara acak, peluang terambil dua dadu berlainan warna adalah a/b dengan a/b merupakan bilangan pecahan yang paling sederhana. Nilai a + b adalah…
Pembahasan
Kemungkinan terambil dua dadu berlainan warna sebagai berikut:
- Dadu hitam-cokelat
- Dadu hitam-merah
- Dadu cokelat-merah
Jumlah seluruh dadu dalam kantong n(S) = 3 + 2 + 2 = 7.
banyak cara mengambil 1 dadu hitam dari 3 dadu = 3
banyak cara mengambil 1 dadu cokelat dari 2 dadu = 2
banyak cara mengambil 1 dadu merah dari 2 dadu = 2
Banyak cara mengambil dadu hitam-cokelat = 3 x 2 = 6
Banyak cara mengambil dadu hitam-merah = 3 x 2 = 6
Banyak cara mengambil dadu cokelat-merah = 2 x 2 = 4.
Berdasarkan perhitungan diatas, banyak cara yang paling sedikit adalah mengambil dadu cokelat-merah yaitu sebanyak 4. Peluang mengambil dadu cokelat-merah = 4/7. Jadi a =4 dan b = 7 sehingga a + b = 4 + 7 = 11.