Contoh soal dinamika gerak partikel nomor 1
Pada grafik berikut.

Jika massa Susan dan sepeda adalah 60 kg dan gaya gesek antara sepeda dan tanah selalu sama. Tentukan:
a. gaya yang diberikan Susan pada detik ke-1 sampai detik ke-4,
b. gaya yang diberikan Susan saat detik ke-4 sampai ke-10 (g = 10 m/s2).
Pembahasan
Gaya yang bekerja pada susan dan sepeda sebagai berikut.

Tentukan fg, berdasarkan gambar di atas diperoleh.
320 N – mg sin θ – fg = 0
320 N – 60 kg . 10 m/s2 sin 30o – fg = 0
320 N – 300 N – fg = 0
fg = 320 N – 300 N = 20 N
Jawaban pertanyaan (a).
Percepatan detik ke-1 sampai detik ke-4 sebagai berikut.
a =
a = m/s2 = – 1 m/s2
Besar gaya yang diberikan Susan pada detik ke-1 sampai 4 sebagai berikut.
ΣF = m . a
Fsusan – mg sin θ – fg = 60 kg . (-1 m/s2)
Fsusan – 300 N – 20 N = – 60 N
FSusan = -60 N + 320 = 260 N
Jawaban pertanyaan (b).
FSusan = mg sin θ + fg
FSusan = 300 N + 20 N = 320 N
Contoh soal dinamika gerak partikel nomor 2

Sebuah bola pejal akan dijatuhkan dari sebuah gedung dengan menggunakan sistem katrol sepeti gambar di samping. Balok A memiliki massa 20 kg dan bola B bermassa 10 kg. Jika mula-mula bola B diam dan jaraknya dari tanah adalah 10 m. Tentukan waktu yang diperlukan bola B hingga menyentuh tanah jika bola B dilepaskan.
Pembahasan
Percepatan benda dan bola sebagai berikut.
wB – fg = (mA + mB) a
10 kg . 10 m/s2 – 0,2 . 20 kg . 10 m/s2 = (20 kg + 10 kg) a
100 N – 40 N = 30 kg . a
a = = 2 m/s2
Waktu yang diperlukan bola B hingga menyentuh tanah sebagai berikut.
S = a t2
10 m = 2 m/s2 . t2
t = s
Contoh soal dinamika gerak partikel nomor 3
Sebuah kereta bergerak pada lintasan lurus yang pergerakannya ditunjukkan seperti pada grafik tersebut.
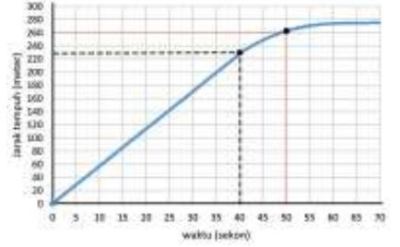
Pada detik ke 0 hingga 40 kereta mengalami gaya hambat sebesar 1.000 N. Dengan menganggap gaya dari kereta adalah konstan dan massa kereta adalah 1.000 kg, perkirakan gaya hambat pada kereta setelah bergerak lebih dari 40 detik.
Pembahasan
Hitung percepatan pada selang waktu 40 – 50 s dengan cara dibawah ini.
s = vot + at2
260 m – 230 m = . (50 s – 40 s) +
a (50 s – 40 s)2
30 m = 5,75 m/s . 10 s + a (10 s)2
30 m = 57,5 m + a . 50 s2
a . 50 s2 = 30 m – 57,5 m = – 27,5 m
a = = – 0,55 m/s2 (tanda negatif menunjukkan perlambatan).
Contoh soal dinamika gerak partikel nomor 4
Dua buah benda dengan massa yang sama yaitu 500 gram saling mendekat seperti ditunjukkan pada gambar berikut. Kedua benda tersebut kemudian bertumbukan dan memiliki waktu kontak sekitar 500 mili-sekon.

Dari diagram di samping, tentukan:
a. kecepatan kedua bola setelah tumbukan
b. gaya rata-rata antara dua benda saat bertumbukan
c. energi yang hilang saat bertumbukan
Pembahasan
Jawaban pertanyaan (a).
Gunakan hukum kekekalan momentum.
Untuk arah sumbu x diperoleh persamaan sebagai berikut.
m1 . v1x + m2 . v2x = m1 . m1x‘ + m2 . v2x‘ (karena m1 = m2 maka persamaan menjadi)
v1x + v2x = v1x‘ + v2x‘
10 m/s – 5 m/s = v1‘ cos 45o + v2‘ cos 30o
5 m/s = v1‘ + v2‘
10 m/s = v1‘ + v2‘
… (pers. 1)
Untuk arah sumbu y diperoleh persamaan sebagai berikut.
m1 . v1y + m2 . v2y = m1 . m1y‘ + m2 . v2y‘ (karena m1 = m2 maka persamaan menjadi)
v1y + v2y = v1y‘ + v2y‘
0 m/s + 0 m/s = v1‘ sin 45o + (-v2‘ sin 30o)
0 m/s = v1‘ –
v2‘
v2‘ = v1‘ … (pers. 2)
Subtitusi v2‘ ke persamaan 1.
10 m/s = v1‘ + v1‘
10 m/s = v1‘ ()
10 m/s = v1‘ () = v1‘ (1,41 + 2,45) = 3,86 v1‘
v1‘ = m/s = 2,59 m/s
v2‘ = v1‘ = 2,59 m/s . 1,41 = 3,65 m/s
Jawaban pertanyaan (b)
Perubahan momentum arah mendatar (sumbu x) sebagai berikut.
Fx . Δt = m1 (v1x‘ – v1)
Fx . (0,05 s) = 0,5 kg (2,59 m/s cos 45o) – 10 m/s)
Fx . (0,05 s) = 0,5 kg (1,83 m/s – 10 m/s) = 0,5 kg . (-8,17 m/s)
Fx = N = -81,7 N
Perubahan momentum arah mendatar (sumbu x) sebagai berikut.
Fx . Δt = m1 (v1y‘ – v1y)
Fx . (0,05 s) = 0,5 kg (2,59 m/s sin 45o) – 0 m/s)
Fx . (0,05 s) = 0,5 kg (1,83 m/s)
Fx = N = 18,3 N
Resultan gaya saat bertumbukan sebagai berikut.
|F| =
|F| =
|F| = N =
N = 83,7 N
Jawaban pertanyaan (c).
Ehilang = ( (v12 + v22) –
((v1‘)2 + (v2‘)2))
Ehilang = ( 0,5 kg ((10 m/s)2 + (-5 m/s)2) –
0,5 kg ((2,59 m/s)2 + (3,65 m/s)2))
Ehilang = 0,25 kg ((100 + 25) (m/s)2 – ((6,7 + 13,3) (m/s)2))
Ehilang = 0,25 kg (125 – 20) m2/s2 = 0,25 kg . 105 m2/s2 = 26,25 J
Contoh soal dinamika gerak partikel nomor 5
Sebuah tongkat homogen bermassa 2 kg ditahan oleh dua buah tali seperti yang ditunjukkan pada gambar berikut.
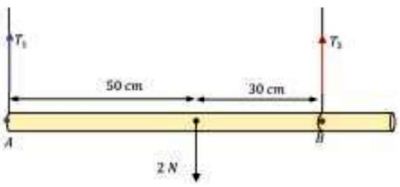
Dari sistem di atas, tentukan:
a. momen titik pusat massa terhadap B.
b. tegangan pada tali T1 dan T2
c. percepatan pusat massa dari tongkat apabila tali di titik B di potong. Momen inersia tongkat terhadap titik tumpu A adalah 6,7 kgm2.
Pembahasan
