Kumpulan rumus dinamika rotasi dan keterangan simbol

Postingan ini membahas kumpulan rumus dinamika rotasi seperti rumus momen gaya, momen inersia, momentum sudut, energi kinetik rotasi, dan energi kinetik rotasi yang disertai dengan keterangan simbol.

Rumus momen gaya

→ τ = F . L
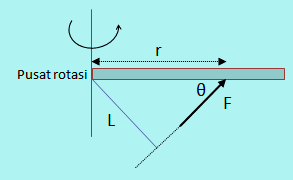
→ τ = F . r . sin θ

Keterangan simbol:

• τ = Momen gaya atau torsi (Nm)
• F = gaya (N)
• L = lengan gaya (m)
• r = panjang batang di ukur dari pusat rotasi hingga ujung/ pangkal gaya (m).
• θ = sudut antara gaya dengan lengan gaya.

Jika pada benda bekerja n buah gaya maka rumus momen gaya sebagai berikut:

→ ∑ τ = τ1 + τ2 + τ3 + … + τn
→ ∑ τ = F1 . L1 + F2 . L2 + F3 . L3 + … + Fn . Ln

Rumus momen inersia partikel

→ I = m . r2

Keterangan simbol:

• I = momen inersia (kg.m2)
• m = massa partikel (kg)
• r = jarak partikel ke sumbu rotasi (m)

Rumus momen inersia sistem partikel

→ ∑ I = I1 + I2 + I3 + … + In
→ ∑ I = m1 . r12 + m2 . r22 + m3 . r32 + … + mn . rn2

Keterangan:

• I = momen inersia partikel 1, 2, 3, n (kg.m2)
• m1, m2, m3, mn = massa partikel 1, 2, 3, n (kg)
• r1, r2, r3, rn = jarak partikel 1, 2, 3, n ke pusat rotasi (m)

Rumus momen inersia silinder berongga poros di sumbu

→ I = m . R2

Rumus momen inersia silinder pejal poros disumbu

→ I =

1

2

m . R2

Keterangan:

• I = momen inersia (kg.m2)
• m = massa silinder (kg)
• R = jari-jari silinder (m)

Rumus momen inersia batang tipis poros disalah satu ujung

→ I =

1

3

M . L2

Rumus momen inersia batang tipis poros di tengah

→ I =

1

12

M . L2

Keterangan:

• M = massa batang (kg)
• L = panjang batang (m)

Rumus momen inersia bola tipis poros di diameter

→ I =

2

3

M . R2

Rumus momen inersia bola pejal poros di diameter

→ I =

2

5

M . R2

Keterangan:

• M = massa bola (kg)
• R = jari-jari bola (m)

Hukum II Newton rotasi

→ ∑ τ = I . α

Keterangan:

• τ = torsi (Nm)
• I = momen inersia
• α = percepatan sudut (rad/s2 )

Rumus momentum sudut

→ L = I . ω

Keterangan:

• L = momentum sudut (kg.m2 .s-1 )
• I = momen inersia (kg.m2 )
• ω = kecepatan sudut (rad/s)

Rumus hukum kekekalan momentum sudut

→ L1 = L2
→ I1 . ω1 = I2 . ω2

Rumus energi kinetik rotasi

→ Ek =

1

2

. I . ω2

Rumus energi kinetik menggelinding

→ Ek =

1

2

. m . v2 +

1

2

. I . ω2

Keterangan:

• Ek = energi kinetik (joule)
• m = massa (kg)
• I = momen inersia (kg.m2 )
• v = kecepatan linear (m/s)
• ω = kecepatan sudut (rad/s)

Rumus pusat massa

→ X_pm =

x₁ . m₁ + x₂ . m₂ + x₃ . m₃ + … + x_n . m_n

m₁ + m₂ + m₃ + … + m_n

→ Y_pm =

y₁ . m₁ + y₂ . m₂ + y₃ . m₃ + … + y_n . m_n

m₁ + m₂ + m₃ + … + m_n

Keterangan:

• X_pm = pusat massa di sumbu X (kg)
• Y_pm = pusat massa di sumbu Y (kg)
• m₁, m₂, m₃, m_n = massa partikel 1, 2, 3, n (kg)
• x₁, x₂, x₃, x_n = titik koordinat x partikel 1, 2, 3, n.
• y₁, y₂, y₃, y_n = titik koordinat y partikel 1, 2, 3, n.

Rumus titik berat bidang homogen

Bidang satu dimensi

→ X_w =

x₁ . L₁ + x₂ . L₂ + x₃ . L₃ + … + x_n . L_n

L₁ + L₂ + L₃ + … + L_n

→ Y_w =

y₁ . L₁ + y₂ . L₂ + y₃ . L₃ + … + y_n . L_n

L₁ + L₂ + L₃ + … + L_n

Bidang dua dimensi

→ X_w =

x₁ . A₁ + x₂ . A₂ + x₃ . A₃ + … + x_n . A_n

A₁ + A₂ + A₃ + … + A_n

→ Y_w =

y₁ . A₁ + y₂ . A₂ + y₃ . A₃ + … + y_n . A_n

A₁ + A₂ + A₃ + … + A_n

Bidang tiga dimensi

→ X_w =

x₁ . V₁ + x₂ . V₂ + x₃ . V₃ + … + x_n . V_n

V₁ + V₂ + V₃ + … + V_n

→ Y_w =

y₁ . V₁ + y₂ . V₂ + y₃ . V₃ + … + y_n . V_n

V₁ + V₂ + V₃ + … + V_n

Keterangan:

• L₁, L₂, L₃ = Panjang benda 1, 2, 3.
• A₁, A₂, A₃ = luas bidang 1, 2, 3.
• V₁, V₂, V₃ = volume benda 1, 2, 3.

Syarat kesetimbangan statis benda tegar

1. Στ = 0
2. ∑F = 0