Contoh soal segitiga pascal atau barisan bilangan tingkat dua

Barisan bilangan pada segitiga pascal merupakan barisan bilangan khusus tingkat dua. Mengapa disebut barisan bilangan tingkat dua ?. Jawabannya karena barisan bilangan tersebut mempunyai selisih yang tetap atau sama pada pola kedua. Ada dua cara menyelesaikan soal barisan bilangan tingkat dua. Pertama menggunakan rumus segitiga pascal yaitu sebagai berikut.

Cara kedua menyelesaikan soal barisan bilangan tingkat dua yaitu dengan menggunakan rumus an² + bn + c dengan a, b, c, ∈ R. Untuk memperoleh suku ke n, nilai n = 1, n = 2, dan n = 3 disubtitusikan ke rumus an² + bn + c maka diperoleh sistem persamaan dengan tiga variabel atau peubah.

Untuk lebih jelasnya, dibawah ini diberikan beberapa contoh soal segitiga pascal atau barisan bilangan tingkat dua yang disertai pembahasannya.

Contoh soal 1

Tentukan suku ke-n dari barisan bilangan 1, 2, 4, 7, 11, 16, … dengan menggunakan cara segitiga pascal.

Pembahasan

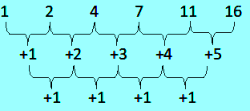
Berdasarkan gambar diatas, selisih terakhir barisan bilangan adalah +1. Dengan menggunakan segitiga pascal diperoleh:

U1 = 1 = ( $\frac {1} {2}$ x 1 x 0) + 1
U2 = 2 = ( $\frac {1} {2}$ x 2 x 1) + 1
U3 = 3 = ( $\frac {1} {2}$ x 3 x 2) + 1
U4 = 7 = ( $\frac {1} {2}$ x 4 x 3) + 1
U5 = 11 = ( $\frac {1} {2}$ x 5 x 4) + 1
U6 = 16 = ( $\frac {1} {2}$ x 6 x 5) + 1
Un = ( $\frac {1} {2}$ x n x (n – 1)) + 1
Un = $\frac {1} {2}$ n² – $\frac {1} {2}$ n + 1

Jadi suku ke-n = Un = $\frac {1} {2}$ n² – $\frac {1} {2}$ n + 1

Contoh soal 2

Tentukan suku ke n barisan bilangan 1, 3, 7, 13, 21, 31, … dengan menggunakan rumus Un = an² + bn + c.

Pembahasan

Pada barisan bilangan diatas diketahui:

U1 = 1
U2 = 3
U3 = 7

Cara menjawab soal ini sebagai berikut:

Un = an² + bn + c
U1 = a . 1² + b . 1 + c = a + b + c = 1 (persamaan 1)
U2 = a . 2² + b . 2 + c = 4a + 2b + c = 3 (persamaan 2)
U3 = a . 3² + b . 3 + c = 9a + 3b + c = 7 (persamaan 3)

Kemudian eliminasi persamaan 1 dengan 2 dan persamaan 2 dengan 3 dan hasilnya sebagai berikut:

Barisan bilangan tingkat 2 — Pembahasan soal barisan bilangan tingkat dua

Maka suku ke-n soal diatas Un = 1 . n² – 1 . n + 1 = n² – n + 1.

Contoh soal 3

Tentukan suku ke-n dari barisan bilangan 3, 4, 6, 9, 13, 18, … dengan menggunakan segitiga pascal.

Pembahasan

Selisih terakhir barisan bilangan diatas adalah +1. Dengan menggunakan rumus segitiga pascal diperoleh:

U1 = 3 = ( $\frac {1} {2}$ x 1 x 0) + 3
U2 = 4 = ( $\frac {1} {2}$ x 2 x 1) + 3
U3 = 6 = ( $\frac {1} {2}$ x 3 x 2) + 3
U4 = 9 = ( $\frac {1} {2}$ x 4 x 3) + 3
U5 = 13 = ( $\frac {1} {2}$ x 5 x 4) + 3
U6 = 18 = ( $\frac {1} {2}$ x 6 x 5) + 3
Un = ( $\frac {1} {2}$ x n x (n – 1)) + 3
Un = $\frac {1} {2}$ n² – $\frac {1} {2}$ n + 3

Contoh soal 4

Tentukan suku ke-n dari barisan bilangan 4, 5, 7, 10, 14, 19, … dengan menggunakan rumus an² + bn + c.

Pembahasan

Diketahui:

U1 = 4
U2 = 5
U3 = 7

Dengan menggunakan rumus an² + bn + c diperoleh:

U1 = a . 1² + b . 1 + c = a + b + c = 4 (persamaan 1)
U2 = a . 2² + b . 2 + c = 4a + 2b + c = 5 (persamaan 2)
U3 = a . 3² + b . 3 + c = 9a + 3b + c = 7 (persamaan 3)

Maka suku ke-n soal diatas Un = $\frac {1} {2}$ n² – $\frac {1} {2}$ n + 4.

Contoh soal 5

Tentukan suku ke n barisa bilangan 1, 4, 10, 19, 31, 46, … dengan menggunakan segitiga pascal.

Pembahasan

Selisih terakhir adalah +3. Dengan menggunakan rumus segitiga pascal diperoleh:

U1 = 1 = ( $\frac {3} {2}$ x 1 x 0) + 1
U2 = 4 = ( $\frac {3} {2}$ x 2 x 1) + 1
U3 = 10 = ( $\frac {3} {2}$ x 3 x 2) + 1
U4 = 19 = ( $\frac {3} {2}$ x 4 x 3) + 1
U5 = 31 = ( $\frac {3} {2}$ x 5 x 4) + 1
U6 = 46 = ( $\frac {3} {2}$ x 6 x 5) + 1
Un = ( $\frac {3} {2}$ x n x (n – 1)) + 1
Un = $\frac {3} {2}$ n² – $\frac {3} {2}$ n + 1

Contoh soal 6

Tentukan suku ke n barisan bilangan 5, 8, 13, 20, 29, 40, … dengan menggunakan segitiga pascal.

Pembahasan

Selisih terakhir barisan bilangan diatas adalah +2. Dengan menggunakan segitiga pascal diperoleh.

U1 = 5 = ( $\frac {2} {2}$ x 1 x 0) + 5
U2 = 8 = ( $\frac {2} {2}$ x 2 x 1) + 6
U3 = 13 = ( $\frac {2} {2}$ x 3 x 2) + 7
U4 = 20 = ( $\frac {2} {2}$ x 4 x 3) + 8
U5 = 29 = ( $\frac {2} {2}$ x 5 x 4) + 9
U6 = 40 = ( $\frac {2} {2}$ x 6 x 5) + 10
Un = ( $\frac {2} {2}$ x n x (n – 1)) + (n + 4)
Un = $\frac {2} {2}$ n² – $\frac {2} {2}$ n + n + 4
Un = n² + 4

Itulah 6 contoh soal segitiga pascal atau barisan bilangan tingkat 2.

Contoh soal segitiga pascal atau barisan bilangan tingkat dua

Tinggalkan Balasan Batalkan balasan