Contoh soal integral substitusi dan pembahasannya

Postingan ini membahas contoh soal integral dengan substitusi dan pambahasannya. Beberapa bentuk integral yang rumit dapat dikerjakan secara sederhana dengan melakukan substitusi tertentu ke dalam fungsi yang diintegralkan tersebut. Diantara bentuk integral yang dapat dikerjakan dengan substitusi adalah bentuk ∫ (fx)n d(fx).

Coba perhatikan bentuk ∫xn dx. Bentuk ini telah kita pelajari pada postingan sebelumnya. Bagaimana jika variabel diganti dengan fungsi, misalnya fx?. Bentuk ini akan menjadi ∫ (fx)n d(fx).

Untuk menyelesaikan suatu integral yang dapat disederhanakan menjadi bentuk ∫ (fx)n d(fx), dapat dilakukan substitusi u = fx. Dengan subtitusi u = fx diperoleh integral sebagai berikut:

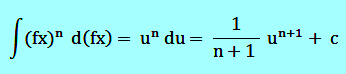
Untuk lebih jelasnya, dibawah ini diberikan beberapa contoh soal integral dengan substitusi dan pembahasannya.

Contoh soal 1 (UN 2018 IPA)

Pembahasan

Misal u = 2 – x3
du = -3x2 dx atau x2 dx = – 1/3 du
∫ (2 – x3)1/2 x2 dx = ∫ u1/2 . -1/3 du

∫ u1/2 . -1/3 du =

1

1/2 + 1

u1/2 + 1 . -1/3 + C
=

1

3/2

. u3/2 . – 1/3 + C = –

2

9

(2 – x3)3/2 + C
Soal ini jawabannya C.

---

Contoh soal 2 (UN 2018 IPA)

Pembahasan

Misal u = x3 + 2
du = 3x2 dx atau 2x2 = 2/3 du
∫ (x3 + 2)5 2x3 dx = ∫ u5 . 2/3 du

∫ u5 . 2/3 du =

1

5 + 1

u5 + 1 . 2/3 + C
1/6 . u6 . 2/3 + C = 1/9 (x3 + 2)6 + C
Soal ini jawabannya B.

---

Contoh soal 3 (UN 2017 IPA)

Pembahasan

Misalkan u = x2 + 4x – 3
du = (2x + 4) dx = 2 (x + 2) dx
(x + 2) dx = 1/2 du
Jadi integral diatas dapat ditulis menjadi ∫ 1/ u1/2 . 1/2 du atau ∫ u-1/2 . 1/2 du
Catatan = akar = pangkat 1/2.

=

1

-1/2 + 1

u-1/2 + 1 . 1/2 + C
=

1

1/2

u1/2 . 1/2 + C
= u1/2 + C
= √

x2 + 4x – 3

+ C
Soal ini jawabannya A.

---

Contoh soal 4 (UN 2015 IPA)

Pembahasan

Misal u = 2x3 + 5
du = 6x2 dx = 2 . 3x2 dx
3x2 dx = 1/2 du
Jadi integral diatas dapat ditulis sebagai berikut:

∫ √ u   . 1/2 du = u1/2 . 1/2 du
=

1

1/2 + 1

u1/2 + 1 . 1/2 + C
3/2 u3/2 . 1/2 + C = 3/4 . u3/2 + C
= 3/4 (2x3 + 5)√

2x3 + 5

+ C
Soal ini jawabannya A.

---

Contoh soal 5

Carilah hasil integral berikut.

∫

(4x3 – 6x2) dx

x4 – 2x3 + 5

Pembahasan

Misal u = x4 – 2x3 + 5
du = 4x3 – 6x2
Jadi integral diatas ditulis menjadi:
∫ u du = 1/(1 + 1) u1 + 1 + C = 1/2 . u2
= 1/2 (x4 – 2x3 + 5)2.

---

Contoh soal 6

Hitunglah integral dari

Pembahasan

Misalkan u = x2 – 4x + 5
du = (2x – 4) dx
Jadi integral diatas menjadi:

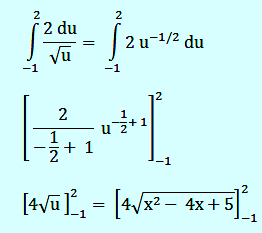
Kemudian masukkan batas atas dan bawah sehingga diperoleh hasil sebagai berikut:

= (4 √

22 – 4 . 2 + 5)

– (4 √

(-1)2 – 4 (-1) + 5)

= 4 – 4 √ 10   = 4 (1 – √ 10   )