Contoh soal regresi linear nomor 1
Tabel berikut menunjukkan banyak tempat duduk terhadap biaya per jam dari tiga model pesawat terbang yang digunakan oleh maskapai Garuda Indonesia.

Persamaan garis regresi mana yang lebih tepat untuk memprediksi banyak tempat duduk terhadap biaya.
ŷ = 367000 + 16000x atau ŷ = 300000 + 16000x
Pembahasan
Misalkan banyak tempat duduk = x, dan biaya = y. Kemudian kita hitung jumlah kuadrat residunya dengan cara dibawah ini.
- ŷ = 367000 + 16000x
- (x = 50) maka ŷ = 367000 + 16000 . 50 = 1.167.000
- (x = 100) maka ŷ = 367000 + 16000 . 100 = 1.967.000
- (x = 150) maka ŷ = 367000 + 16000 . 150 = 2.767.000

- ŷ = 300000 + 16000x
- (x = 50) maka ŷ = 300000 + 16000 . 50 = 1.100.000
- (x = 100) maka ŷ = 300000 + 16000 . 100 = 1.900.000
- (x = 150) maka ŷ = 300000 + 16000 . 150 = 2.700.000
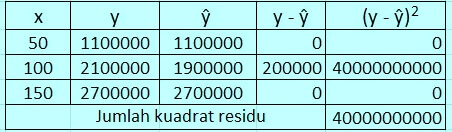
Jumlah kuadrat residu ŷ = 367000 + 16000x lebih kecil daripada jumlah kuadrat residu ŷ = 300000 + 16000x. Artinya persamaan garis regresi ŷ = 367000 + 16000x lebih tepat dari pada ŷ = 300000 + 16000x.
Contoh soal regresi linear nomor 2
Seorang siswa menyelidiki hubungan antara harga (y rupiah) dari 100 gram cokelat dan persentase kandungan cokelat (x %). Data yang diperoleh disajikan pada tabel berikut.

a. Gambarlah diagram pencar dari data tabel tersebut.
Jika diketahui bahwa persamaan garis regresinya adalah ŷ = 1700 + 154x
b. Gambarlah garis regresinya pada diagram pencar.
Siswa melihat bahwa ada satu merek cokelat yang harganya terlalu tinggi.
c. Merek cokelat mana yang dimaksud oleh siswa tersebut? jelaskan alasannya.
d. Siswa tersebut ingin memberikan saran harga yang cocok untuk cokelat tersebut. Berapakah prediksi harga yang cocok?.
Pembahasan
- Jawaban soal (a) sebagai berikut.

- Jawaban soal (b) sebagai berikut.

- Jawaban soal (c) sebagai berikut.
Merek cokelat yang harganya terlalu tinggi adalah Merek D (35 % cokelat dengan harga Rp10.000,00), karena berada terlalu tinggi dengan garis regresi.
- Jawaban soal (d) sebagai berikut.
Untuk menentukan harga yang cocok cokelat D, subtitusi nilai x = 35 ke persamaan garis regresi ŷ = 1700 + 154x. Hasilnya sebagai berikut.
- ŷ = 1700 + 154x
- ŷ = 1700 + 154 . 35
- ŷ = 1700 + 5390
- ŷ = 7090
Jadi harga yang cocok untuk harga cokelat D = Rp7.090,00.
Contoh soal regresi linear nomor 3
Tabel berikut ini berisi informasi dari 12 siswa SMA mengenai rata-rata waktu yang digunakan per hari dalam menggunakan media sosial (Facebook, Twitter, dan lain-lain) dan internet untuk bersosialisasi dan hiburan, dan nilai mereka.

1. Gambarkan diagram pencar dari data diatas.
2. Apakah diagram pencarnya memberikan indikasi bahwa ada hubungan linear antara rata-rata waktu untuk media sosial dan internet dengan nilai?.
3. Tentukan persamaan garis regresinya. Ikuti tahapan berikut ini.
a. Hitunglah nilai ̄x dan ̄y.
b. Hitunglah nilai SSxy dan SSxx.
c. Hitunglah nilai b, gradien garis regresi, menggunakan hasil dari a) dan b).
d. Hitunglah nilai a, titik potong sumbu y, menggunakan hasil a) dan c).
e. Tentukan persamaan garis regresinya dengan menggunakan hasil dari c) dan d).
4. Interpretasikan masing-masing arti nilai a dan b yang ditemukan pada nomor 3.
5. Hitunglah prediksi nilai siswa yang menggunakan rata-rata waktu 3,8 jam per hari untuk media sosial dan internet menggunakan persamaan garis regresi yang ditemukan pada nomor 3.
6. Hitunglah prediksi nilai siswa yang menggunakn rata-rata waktu 16 jam per hari untuk media sosial dan internet menggunakan persamaan garis regresi yang ditemukan pada nomor 3. Berikan komentar hasil yang ditemukan.
Pembahasan
Jawaban soal (1) sebagai berikut.

Jawaban soal (2) sebagai berikut.
Ada indikasi hubungan antara waktu rata-rata dengan nilai linear.
Jawaban soal (3) sebagai berikut.
- ̄x =
- ̄x =
= 3,93
- ̄y =
- ̄y =
= 74,33
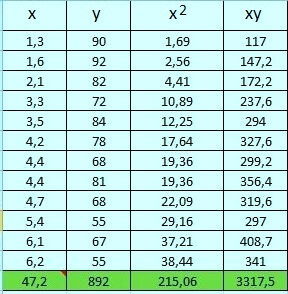
- SSxy =
- SSxy = 3317,5 –
- SSxy = 3317,5 –
= -191
- SSxx =
- SSxx = 215,06 –
- SSxx = 215,06 – 185,65 = 29,41
- b =
- b =
= -6,49
- a = ̄y – b̄x
- a = 74,33 – (-6,49) . 3,93
- a = 74,33 + 25,5 = 99,83
- ŷ = 99,83 – 6,49x
Jawaban soal (4) sebagai berikut.
Arti dari nilai a = 99,83 adalah jika siswa tidak menggunakan media sosial dan internet sama sekali maka prediksi nilainya adalah 99,83. Sedangkan arti dari nilai b = -6,49 menunjukkan menggunakan media sosial dan internet selama satu jam per hari dapat menurunkan nilai sebesar 6,49.
Jawaban soal (5) sebagai berikut.
- ŷ = 99,83 – 6,49x
- ŷ = 99,83 – 6,49 . 3,8
- ŷ = 99,83 – 24,662 = 75,168
Jadi prediksi nilai jika menggunakan media sosial dan internet selama 3,8 jam per hari adalah 75,168.
Jawaban soal (6) sebagai berikut.
- ŷ = 99,83 – 6,49x
- ŷ = 99,83 – 6,49 . 16
- ŷ = 99,83 – 103,84 = -4,01
Jadi prediksi nilai jika menggunakan media sosial dan internet selama 16 jam per hari adalah -4,01. Artinya, menggunakan media sosial dan internet dalam waktu yang lama dalam sehari dapat berakibat buruk pada nilai sekolah.
Contoh soal regresi linear nomor 4
Pada saat kondisi mendadak, para pengendara mobil memerlukan waktu yang berbeda-beda untuk dapat bereaksi untuk menginjak rem mobil. Jarak yang diperlukan hingga terjadi reaksi menginjak rem disebut jarak reaksi. Tabel berikut ini memberikan informasi mengenai jarak reaksi dari mobil yang melaju dengan kecepatan yang berbeda-beda.
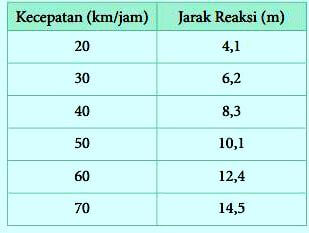
a. Gambarlah diagram pencar dari data diatas.
b. Apakah diagram pencarnya memberikan indikasi bahwa ada hubungan linear antara kecepatan dengan jarak reaksi?.
c. Tentukan persamaan garis regresinya.
d. Interpretasikan nilai a dan b yang diperoleh pada bagian c).
e. Hitunglah prediksi jarak reaksi jika suatu mobil bergerak dengan kecepatan 35 km/jam.
f. Hitunglah prediksi jarak reaksi jika suatu mobil bergerak dengan kecepatan 55 km/jam.
Pembahasan
Jawaban soal (a) sebagai berikut.

Jawaban soal (b) sebagai berikut.
Ada indikasi hubungan linear antara kecepatan dengan jarak reaksi.
Jawaban soal (c) sebagai berikut.
- ̄x =
- ̄x =
= 45
- ̄y =
- ̄y =
= 9,266

- SSxy =
- SSxy = 2839 –
- SSxy = 2839 –
= 392,6
- SSxx =
- SSxx = 13696 –
- SSxx = 13696 – 11616 = 2080
- b =
- b =
= 0,188
- a = ̄y – b̄x
- a = 9,266 – (0,188) . 45
- a = 9,266 – 8,46 = 0,8
- ŷ = 0,8 + 0,188x
Jawaban soal (d) sebagai berikut.
Arti dari a = 0,8 adalah jika kecepatannya nol atau diam maka jarak reaksinya adalah 0,8 m. Sedangkan arti dari b = 0,188 adalah jika kecepatan bertambah 1 km/jam maka jarak reaksi bertambah sebesar 0,188 m.
Jawaban soal (e) sebagai berikut
ŷ = 0,8 + 0,188 . 35 = 7,38. Jadi jika kecepatan = 35 km/jam maka jarak reaksi = 7,38 m.
Jawaban soal (f) sebagai berikut.
ŷ = 0,8 + 0,188 . 55 = 7,38. Jadi jika kecepatan = 35 km/jam maka jarak reaksi = 11,14 m.
Contoh soal regresi linear nomor 5
Tabel berikut ini data mengenai rata-rata tinggi badan anak perempuan yang berumur dari 2-14 tahun.

a. Gambarlah diagram pencar dari data diatas.
b. Apakah diagram pencarnya memberikan indikasi bahwa ada hubungan linear antara umur dengan rata-rata tinggi badan?.
c. Tentukan persamaan garis regresinya.
d. Interpretasikan nilai a dan b yang diperoleh pada bagian c).
e. Hitunglah prediksi tinggi badan anak perempuan yang berumur 5,8 tahun.
f. Hitunglah prediksi tinggi badan seorang perempuan yang sudah berumur 30 tahun.
g. Berikan komentar mengenai reliabilitas nilai perkiraan di bagian f).
Pembahasan
Jawaban soal (a) sebagai berikut.

Jawaban soal (b) sebagai berikut.
Ya, ada indikasi hubungannya linear.
Jawaban soal (c) sebagai berikut.
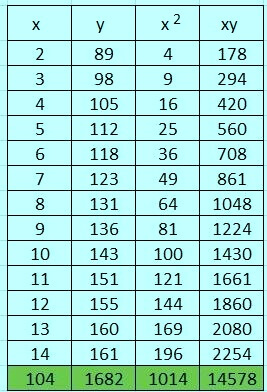
- ̄x = 8
- ̄y = 129,38
- SSxy =
- SSxy = 14578 –
- SSxy = 14578 – 13456 = 1122
- SSxx =
- SSxx = 1014 –
- SSxx = 1014 – 832 = 182
- b =
- b =
= 6,16
- a = ̄y – b̄x
- a = 129,38 – (6,16) . 8
- a = 129,38 – 49,28 = 80,1
- ŷ = 80,1 + 6,16x
Jawaban soal (d) sebagai berikut.
Nilai a = 80,1 artinya jika umur 0 tahun (bayi yang baru lahir) maka tingginya sekitar 80,1 cm. Sedangkan arti b = 6,16 adalah jika umur bertambah 1 tahun maka tinggi badan bertambah 6,16 cm.
Jawaban soal (e) sebagai berikut.
ŷ = 80,1 + 6,16 . 5,8 = 115,8. Jadi prediksi tinggi badan anak perempuan umur 5,8 tahun adalah 115,8 cm.
Jawaban soal (f) sebagai berikut.
ŷ = 80,1 + 6,16 . 30 = 264,9 cm. Jadi prediksi tinggi badan anak perempuan umur 30 tahun adalah 264,9 cm = 2,649 m.
Jawaban soal (g) sebagai berikut.
Melihat hasil (f), hampir mustahil tinggi badan anak perempuan = 2,649 m. Ini artinya persamaan regresi ŷ = 80,1 + 6,16x untuk umur 30 tahun tidak berlaku.
Namun, jika diagram pencar soal (a) kita perhatikan, ketika anak perempuah berusia 13-14 tahun, tinggi badannya mulai stabil. Ini bisa diartikan, jika anak perempuan berusia diatas 14 tahun, maka persamaan ŷ = 80,1 + 6,16x sudah tidak berlaku lagi.
Contoh soal regresi linear nomor 6
Sebuah perusahaan manufaktur mobil ingin menyelidiki bagaimana harga salah satu model mobilnya terdepresiasi (penurunan) seiring bertambahnya usia mobil. Departeman risct di perusahaan mengambil sampel delapan mobil model ini dan mengumpulkan informasi berikut tentang usia (dalam tahun) dan harga (dalam jutaan rupiah) mobil-mobil ini.

a. Gambarlah diagram pencar dari data diatas.
b. Apakah diagram pencarnya memberikan indikasi bahwa ada hubungan linear antara usia dengan harga mobil?.
c. Tentukan persamaan garis regresinya dimana harga sebagai variabel dependen dan usia sebagai variabel independen.
d. Interpretasikan nilai a dan b yang diperoleh pada bagian c).
e. Hitunglah prediksi harga mobil yang berusia 7 tahun.
f. Hitunglah prediksi harga mobil yang berusia 18 tahun.
g. Berikan komentar kalian mengenai hasil perhitungan bagian f).
Pembahasan
Jawaban soal (a) sebagai berikut.

Jawaban soal (b) sebagai berikut.
Ya, ada hubungan linear antara usia dengan harga.
Jawaban soal (c) sebagai berikut.
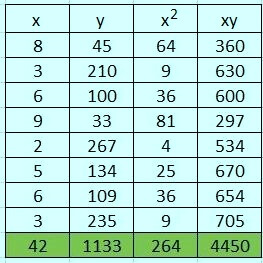
- ̄x = 5,25
- ̄y = 141,62
- SSxy =
- SSxy = 4450 –
- SSxy = 4450 – 5948,25 = -1498,25
- SSxx =
- SSxx = 264 –
- SSxx = 264 – 220,5 = 43,5
- b =
- b =
= -34,44
- a = ̄y – b̄x
- a = 141.62 – (-34,44) . 5,25
- a = 141,62 + 180,81 = 322,43
- ŷ = 322,43 – 34,44x
Jawaban soal (d) sebagai berikut.
a = 322,43 artinya jika usia mobil 0 tahun (masih baru) maka prediksi harganya adalah 322,43 juta. Sedangkan b = -34,44 artinya jika usia mobil bertambah 1 tahun maka harganya turun sebesar 34,44 juta.
Jawaban soal (e) sebagai berikut.
ŷ = 322,43 – 34,44 . 7 = 81,35. Jadi prediksi harga mobil berusia 7 tahun = 81,35 juta.
Jawaban soal (f) sebagai berikut.
ŷ = 322,43 – 34,44 . 18 = -297,49. Jadi prediksi harga mobil berusia 18 tahun = -297,49 juta.
Jawaban soal (g) sebagai berikut.
Harga mobil berusia 18 tahun = – 297,49 juta adalah tidak mungkin. Melihat diagram pencar soal (a), persamaan ŷ = 322,43 – 34,44x mungkin hanya berlaku untuk mobil berusia 9 tahun ke bawah, dan tidak berlaku untuk mobil berusia 9 tahun ke atas.