10 contoh soal rumus suku ke n dan pembahasannya

Contoh soal rumus suku ke n nomor 1

Rumus suku ke n dari barisan 4, 7, 10, 13 adalah …
A. 3n + 1
B. 3n + 2
C. 3n – 1
D. 3n – 2

Pembahasan

Berdasarkan gambar diatas, barisan memiliki beda yang sama, yaitu +3 (b = 3), sehingga merupakan barisan aritmetika. Jadi kita gunakan rumus suku ke n barisan aritmetika, yaitu sebagai berikut.

U_n = a + (n – 1) b
U_n = 4 + (n – 1) 3
U_n = 4 + 3n – 3
U_n = 3n + 1

Soal ini jawabannya A.

Contoh soal rumus suku ke n nomor 2

Rumus suku ke n barisan bilangan 10, 7, 4, …, adalah …
A. U_n = 13 + 3n
B. U_n = 13 – 3n
C. U_n = 3n + 7
D. U_n = 3n – 7

Pembahasan

Berdasarkan gambar diatas, barisan memiliki beda yang sama, yaitu -3 (b = -3) sehingga kita gunakan rumus suku ke n barisan aritmetika sebagai berikut.

U_n = a + (n – 1) b
U_n = 10 + (n – 1) -3
U_n = 10 – 3n + 3
U_n = 13 – 3n

Soal ini jawabannya B.

Contoh soal rumus suku ke n nomor 3

$\frac {1} {2}$ , $\frac {2} {3}$ , $\frac {3} {4}$ , $\frac {4} {5}$ .Pola untuk suku ke n dari barisan tersebut adalah …
A. $\frac {n} {n + 1}$
B. $\frac {n - 1} {n}$
C. $\frac {n^{2} - 1} {n + 1}$
D. $\frac {n + 1} {n + 3}$

Pembahasan

Barisan bilangan untuk pembilang : 1, 2, 3, 4 (b = 1). Jadi rumus suku ke n pembilang sebagai berikut.

U_n = a + (n – 1) b
U_n = 1 + (n – 1) 1
U_n = 1 + n – 1 = n

Barisan bilangan untuk penyebut : 2, 3, 4, 5 (b = 1). Jadi rumus suku ke n penyebut sebagai berikut.

U_n = a + (n – 1) b
U_n = 2 + (n – 1) 1
U_n = 2 + n – 1 = n + 1

Jadi rumus suku ke n barisan diatas = $\frac {rumus pembilang} {rumus penyebut}$ = $\frac {n} {n + 1}$ . Soal ini jawabannya A.

Contoh soal rumus suku ke n nomor 4

Rumus suku ke n dari barisan: -2, 4, -8, 16, …, adalah …
A. (-2)ⁿ
B. (-2)^{n – 1}
C. (2)^-n
D. (2)n
E. -2n

Pembahasan

Barisan diatas memiliki rasio = -2 (r = $\frac {4} {-2}$ = $\frac {-8} {4}$ = $\frac {16} {-8}$ = -2), sehingga merupakan barisan geometri. Jadi kita gunakan rumus suku ke n barisan geometri, yaitu sebagai berikut.

U_n = a . r^{n – 1}
U_n = -2 . (-2)^{n – 1}
U_n = (-2)^{1 + n – 1} = (-2)ⁿ

Soal ini jawabannya A.

Contoh soal rumus suku ke n nomor 5

Rumus suku ke-n dari barisan 0, 2, 6, 12, 20 adalah …
A. n (n + 1)
B. 2n² + 1
C. 2n² – n
D. n² – n

Pembahasan

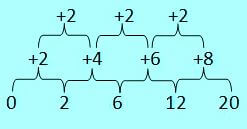
Rumus untuk menjawab soal ini adalah U_n = an² + bn + c.

U₁ = a . 1² + b . 1 + c = 0
a + b + c = 0 … (persamaan 1).
U₂ = a . 2² + b .2 + c = 2
4a + 2b + c = 2 … (persamaan 2).
U₃ = a . 3² + b . 3 + c = 6
9a + 3b + c = 6 … (persamaan 3)

Eliminasi c pada persamaan 1 dan 2.

a + b + c = 0
4a + 2b + c = 2
_________________-
-3a – b = -2
3a + b = 2 …. (persamaan 4)

Eliminasi c pada persamaan 2 dan 3.

4a + 2b + c = 2
9a + 3b + c = 6
_________________-
-5a – b = -4
5a + b = 4 (persamaan 5)

Eliminasi b pada persamaan 4 dan 5.

3a + b = 2
5a + b = 4
____________-
-2a = -2
a = -2 : -2 = 1

Subtitusi a = 1 ke persamaan 5.

5a + b = 4
5 . 1 + b = 4
b = 4 – 5 = -1

Subtitusi a = 1 dan b = -1 ke persamaan 1.

a + b + c = 0
1 + (-1) + c = 0
c = 0

Maka Un = an² + bn + c = 1 . n² + (-1)n + 0 = n² – n. Soal ini jawabannya D.

Contoh soal rumus suku ke n nomor 6

Diketahui barisan sebagai berikut: $\frac {1} {2}$ , $\frac {1} {5}$ , $\frac {1} {10}$ , $\frac {1} {17}$ . Rumus suku ke n dari barisan tersebut adalah …
A. $\frac {1} {n + 1}$
B. $\frac {1} {n + 3}$
C. $\frac {1} {n^{2} + 1}$
D. $\frac {1} {n^{2} - 1}$
E. $\frac {1} {n^{2} + 3}$

Pembahasan

Barisan pembilang = 1, 1, 1, 1. Jadi rumus suku ke n = 1.

Barisan penyebut = 2, 5, 10, 17. Pola barisan tersebut sebagai berikut.

Kemudian gunakan rumus U_n = an² + bn + c.

U₁ = a . 1² + b . 1 + c = 2
a + b + c = 2 ….(persamaan 1)
U₂ = a . 2² + b . 2 + c = 5
4a + 2b + c = 5 …. (persamaan 2)
U₃ = a . 3² + b . 3 + c = 10
9a + 3b + c = 10 …. (persamaan 3)

Eliminasi c persamaan 1 dan 2.

a + b + c = 2
4a + 2b + c = 5
________________-
-3a – b = -3
3a + b = 3 …. (persamaan 4)

Eliminasi c persamaan 2 dan 3.

4a + 2b + c = 5
9a + 3b + c = 10
__________________-
-5a – b = -5
5a + b = 5 …. (persamaan 5)

Eliminasi b persamaan 4 dan 5.

3a + b = 3
5a + b = 5
____________-
-2a = -2
a = -2 : -2 = 1

Subtitusi a = 1 ke persamaan 4.

3a + b = 3
3 . 1 + b = 3
b = 3 – 3 = 0

Subtitusi a = 1 dan b = 0 ke persamaan 1.

a + b + c = 2
1 + 0 + c = 2
c = 2 – 1 = 1

Jadi Un = an2 + bn + c = 1 . n2 + b . 0 + 1 = n² + 1. Jadi, rumus suku ke n = $\frac {1} {n^{2} + 1}$ . Soal ini jawabannya C.

Contoh soal rumus suku ke n nomor 7

Suku ke n dari suatu barisan ditentukan dengan rumus 2ⁿ – 1. Suku ke-5 dari barisan tersebut adalah …
A. 31
B. 32
C. 33
D. 34
E. 35

Pembahasan

U_n = 2ⁿ – 1
U₅ = 2⁵ – 1
U₅ = 32 – 1 = 31

Soal ini jawabannya A.

Contoh soal rumus suku ke n nomor 8

Jika suku ke n dari suatu barisan adalah 5n² – 3, suku ke-7 adalah …
A. 242
B. 177
C. 122
D. 67

Pembahasan

U_n = 5n² – 3
U₇ = 5 . 7² – 3
U₇ = 5 . 49 – 3
U₇ = 245 – 3 = 242

Soal ini jawabannya A.

Contoh soal rumus suku ke n nomor 9

Jumlah n suku pertama dari suatu deret aritmetika adalah Sn = $\frac {n} {2}$ (3n – 17). Rumus umum suku ke n adalah …
A. 3n
B. 3n – 10
C. 3n – 8
D. 3n – 2

Pembahasan

a = S₁ = $\frac {1} {2}$ (3 . 1 – 17)
a = $\frac {1} {2}$ . (-14) = -7
S_n = $\frac {n} {2}$ (a + Un)
$\frac {n} {2}$ (3n – 17) = $\frac {n} {2}$ (-7 + Un)
3n – 17 = -7 + U_n
U_n = 3n – 17 + 7
U_n = 3n – 10

Soal ini jawabannya B.

Contoh soal rumus suku ke n nomor 10

Rumus jumlah n suku pertama deret bilangan 2 + 4 + 6 + 8 + … + U_n adalah …
A. S_n = n² + n
B. S_n = n + 1
C. S_n = 2n + n²
D. S_n = n (n + 1)

Pembahasan

Diketahui:

a = 2
b = 2

Maka rumus S_n sebagai berikut.

S_n = $\frac {n} {2}$ (2a + (n – 1) b)
S_n = $\frac {n} {2}$ (2 . 2 + (n – 1) 2)
S_n = $\frac {n} {2}$ (4 + 2n – 2)
S_n = 2n + n² – n
S_n = n² + n = n (n + 1)

Soal ini jawabannya D.

10 contoh soal rumus suku ke n dan pembahasannya

Tinggalkan Balasan Batalkan balasan