Postingan ini membahas contoh soal cerita segi empat dan penerapan / aplikasi dalam kehidupan yang disertai pembahasannya. Dalam kehidupan sehari-hari banyak sekali dijumpai bangun-bangun segiempat yang ada disekitar kita. Jendela, pintu, bentuk gedung, luas taman, untuk ubin/keramik pada lantai adalah contoh bangun-bangun segi empat. Bentuk segi empat itu bermacam-macam dari yang tidak beraturan sampai yang beraturan seperti jajarangenjang, persegi panjang, belah ketupat, persegi, trapesium dan layang-layang.
Contoh soal 1
Sebuah lapangan berukuran 110 m x 90 m. Ditepi lapangan itu dibuat jalan dengan lebar 3 m mengelilingi lapangan.
a. Tentukan luas jalan tersebut
b. Jika jalan tersebut akan dikeraskan dengan biaya Rp35.000,00 per m2, berapakah biaya seluruh pengerasan jalan itu?
Pembahasan
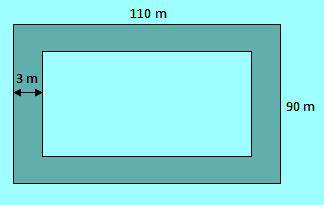
Cara menentukan luas jalan sebagai berikut.
- Luas jalan = Luas persegipanjang besar – Luas persegipanjang kecil
- Luas jalan = 110 m x 90 m – (110 m – 6 m) x (90 m – 6 m)
- Luas jalan = 9.900 m2 – (104 m x 84 m)
- Luas jalan = 9.900 m2 – 8.736 m2 = 1.164 m2
Cara menentukan biaya pengerasan jalan sebagai berikut.
- Biaya pengerasan = luas jalan x Rp35.000,00
- Biaya pengerasan = 1.164 x Rp35.000,00
- Biaya pengerasan = Rp40.740.000,00
Contoh soal 2
Seorang petani mempunyai sebidang tanah berukuran panjang 24 m dan lebar 15 m. Tanah tersebut akan dibuat sebuah kolam berbentuk belah ketupat dengan panjang diagonal-diagonalnya berturut-turut 9 m dan 12 m, sedangkan sisanya akan ditanami pohon pisang. Berapakah luas tanah yang ditanami pohon pisang ?.
Pembahasan
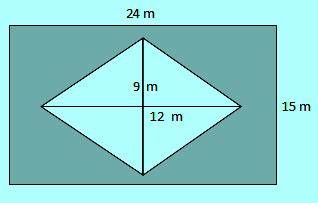
Berdasarkan gambar diatas maka luas tanah yang ditanami pohon pisang sebagai berikut.
- Luas tanah = luas persegipanjang – luas belah ketupat
- Luas tanah = 14 m x 15 m – (1/2 x 9 m x 12 m)
- Luas tanah = 210 m2 – 54 m2 = 156 m2
Contoh soal 3
Diketahui bentuk atap sebuah rumah terdiri atas sepasang trapesium sama kaki dan sepasang segitiga sama kaki. Pada atap berbentuk trapesium panjang sisi sejajarnya masing-masing 5 m dan 3 m. Adapun pada atap berbentuk segitiga panjang alasnya 7 m. Tinggi trapesium = tinggi segitiga = 4 m.
a. Tentukan banyak genteng yang dibutuhkan untuk menutup atap tersebut, jika tiap 1 m2 diperlukan 25 genteng
b. Jika harga 1 buah genteng Rp1.500,00, berapakah biaya yang dibutuhkan seluruhnya ?.
Pembahasan
Banyak genteng yang diperlukan sebagai berikut.
- Banyak genteng = (2 x luas trapesium + 2 x luas segitiga) x 25 genteng/m2
- Banyak genteng = (2 x 1/2 x (5 m + 3 m) x 4 m + 2 x 1/2 x 7 m x 4 m) x 25 genteng/m2
- Banyak genteng = (32 m2 + 28 m2) x 25 genteng/m2
- Banyak genteng = 60 m2 x 25 genteng/m2
- Banyak genteng = 1.500 genteng
Sedangkan biaya yang dibutuhkan = 1.500 x Rp1.500,00 = Rp2.250.000,00.
Contoh soal 4
Danang akan membuat sebuah layang-layang. Ia menyediakan dua potong lidi yang digunakan sebagai kerangka dengan panjang masing-masing 40 cm dan 24 cm. Tentukan luas minimal kertas yang dibutuhkan untuk membuat layang-layang tersebut.
Pembahasan
- Luas kertas = luas layang-layang
- Luas kertas = 1/2 x D1 x D2
- Luas kertas = 1/2 x 40 cm x 24 cm = 480 cm2
Contoh soal 5
Bu Nita memiliki sebidang tanah berbentuk trapesium, sepasang sisi yang sejajar masing-masing panjangnya 35 m dan 45 m. Jika jarak kedua sisi sejajar itu 20 m, hitunglah luas tanah bu Nita.
Pembahasan
- Luas tanah = luas trapesium
- Luas tanah = 1/2 x jumlah sisi sejajar x tinggi
- Luas tanah = 1/2 x (35 m + 45 m) x 20 m
- Luas tanah = 80 m x 10 m = 800 m2
Contoh soal 6
Ifni hendak membuat layang-layang seperti gambar disamping. Jika panjang AC = 50 cm dan panjang BD = 100 cm, berapa cm2 luas kertas yang dibutuhkan ?.
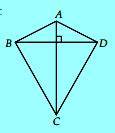
Pembahasan
- Luas kertas = luas layang-layang
- luas kertas = 1/2 x AC x BD
- Luas kertas = 1/2 x 50 cm x 100 cm
- Luas kertas = 2.500 cm2
Contoh soal 7
Diketahui titik O adalah titip potong diagonal-diagonal persegipanjang ABCD yang berukuran 8 cm x 5 cm. Gambarlah diagonal BD dan garis PQ yang memotong sama panjang AB di P dan CD di Q. Arsirlah ΔOPB dan ΔOQD. Jika luas daerah yang diarsir sama dengan seperlima luas seluruh daerah persegi panjang, hitunglah luas daerah APOD.
Pembahasan

- Luas APOD = luas trapesium APOD
- Luas APOD = 1/2 x jumlah sisi sejajar x tinggi
- Luas APOD = 1/2 x (AD + OP) x AP
- Luas APOD = 1/2 x (5 m + 2,5 m) x 4 m
- Luas APOD = 7,5 m x 2 m = 15 m2
Jadi luas APOD = 15 m2.