Postingan ini membahas contoh soal diagram pohon dan pembahasannya. Lalu apa itu diagram pohon. Diagram pohon merupakan salah satu cara menghitung atau mencacah banyak terjadinya suatu kejadian atau banyak anggota suatu kejadian. Misalnya pada pemilihan pengurus OSIS terdapat empat siswa yang lolos untuk putaran akhir, yaitu Adi (A), Budi (B), Cindi (C) dan Dodi (D). Pada putaran akhir akan dipilih dua siswa untuk menduduki posisi ketua dan sekretaris. Pertanyaan yang muncul adalah berapa macam susunan pengurus yang akan menang ?.
Jawabannya adalah dengan menggunakan diagram pohon. Pada putaran akhir terdapat 4 kemungkinan untuk posisi ketua yaitu A, B, C dan D. Setelah satu dari mereka terpilih sebagai ketua, posisi sekretaris adalah salah satu dari siswa yang tidak terpilih sebagai ketua.
Banyaknya susunan posisi ketua dan sekretaris dapat dibentuk dalam diagram pohon seperti gambar dibawah ini.

Jadi banyaknya kemungkinan susunan ketua dan sekretaris OSIS sebanyak 12 yaitu AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC.
Contoh soal diagram pohon
Contoh soal 1
Bilangan yang terdiri dari tiga angka yang berbeda dan bernilai kurang dari 400, akan dibentuk dari angka 3, 4, 5, 6. Banyak bilangan yang terbentuk adalah …
A. 2
B. 3
C. 5
D. 6
E. 9
Pembahasan
Cara menjawab soal ini adalah tentukan angka ratusan yang kurang dari 4, kemudian tentukan angka puluhan dan angka satuan. Selanjutnya susun dengan menggunakan diagram pohon.
- Angka ratusan < 400 adalah 3
- Angka puluhan dan angka satuan adalah 4, 5, 6,
Maka bentuk diagram pohonnya sebagai berikut.
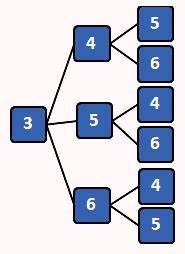
Jadi banyak bilangan kurang dari 400 ada 6 yaitu 345, 346, 354, 356, 364, dan 365. Soal ini jawabannya D.
Contoh soal 2
Bilangan yang terdiri dari tiga angka yang berbeda dan merupakan bilangan genap, akan dibentuk dari angka 2, 3, 4, 5, 6. Banyak bilangan yang terbentuk adalah …
A. 3
B. 5
C. 6
D. 10
E. 36
Pembahasan
Bilangan genap berarti angka terakhirnya bilangan genap yaitu 2, 4 dan 6. Diagram pohon untuk bilangan pertama 3 dan 5 sebagai berikut.

Berdasarkan diagram pohon diatas, banyak bilangan genap yang terbentuk yaitu 9 + 9 = 18. Sedangkan diagram pohon dengan bilangan pertama 2, 4 dan 6 sebagai berikut.

Banyak bilangan yang terbentuk adalah 6 + 6 + 6 = 18. Jadi banyak bilangan yang terbentuk sebanyak 18 + 18 = 36. Soal ini jawabannya E.
Contoh soal 3
Sebuah uang logam dilempar sebanyak empat kali. Banyak cara yang mungkin dari munculnya sisi-sisi uang logam adalah…
A. 4
B. 8
C. 10
D. 16
E. 32
Pembahasan
Misalkan Angka = A dan gambar = G. Dengan menggunakan diagram pohon maka diperoleh hasil sebagai berikut.
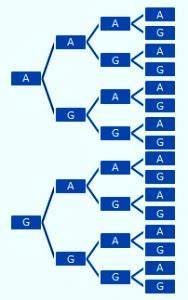
Berdasarkan diagram pohon diatas maka banyak cara yang mungkin munculnya sisi-sisi uang logam adalah 16. Soal ini jawabannya D.
Contoh soal 4
Seorang siswa mempunyai tiga kemeja dan dua celana. Kemeja dan Celana tersebut dapat dipakai ke sekolah. Banyaknya siswa tersebut memasangkan kemeja dan celananya sama dengan …
A. 2
B. 4
C. 5
D. 6
E. 8
Pembahasan
Misalkan celana = C dan kemeja = K maka dengan menggunakan diagram pohon diperoleh hasil sebagai berikut.
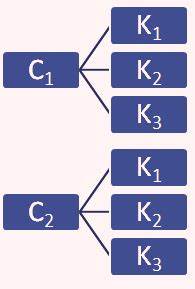
Berdasarkan diagram pohon diatas maka banyak cara memasangkan kemeja dan celana adalah 6. Jadi soal ini jawabannya D.
Contoh soal 5
Dari angka 3, 5, 6, 8, 9 dibuat bilangan yang terdiri dari tiga angka berbeda kurang dari 600. Banyak bilangan yang mungkin adalah …
A. 12
B. 24
C. 36
D. 48
E. 64
Pembahasan
Angka pertama agar tersusun tiga angka kurang dari 600 adalah 3 dan 5. Dengan menggunakan diagram pohon diperoleh hasil sebagai berikut.
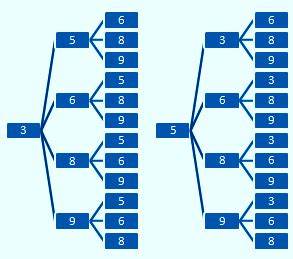
Berdasarkan diagram pohon diatas maka banyak bilangan yang kurang dari 600 adalah 12 + 12 = 24. Soal ini jawabannya B.