Contoh soal sudut keliling dan pembahasannya. Sudut keliling adalah titik sudut yang terletak pada keliling lingkaran yang dibatasi oleh dua buah tali busur. Jika digambarkan sudut keliling seperti dibawah ini.

Sifat-sifat sudut keliling sebagai berikut:
- Jika menghadap busur yang sama, sudut keliling sama dengan 1/2 kali sudut pusat.
- Sudut keliling yang menghadap diameter besarnya 90° atau siku-siku.
- Sudut keliling yang menghadap busur yang sama adalah sama besar.
Contoh soal sudut keliling
Contoh soal 1

Pada gambar dibawah disamping, besar sudut AOB = 110°. Jika panjang AB = BC, maka hitunglah besar sudut ACB.
Pembahasan
Pada soal ini diketahui sudut pusat AOB = 110°. Karena menghadap busur yang sama maka sudut ACB = 1/2 sudut pusat AOB atau ACB = 1/2 . 110° = 55°.
Contoh soal 2
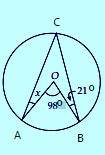
Hitunglah nilai x dari gambar disamping.
Pembahasan
Sudut keliling ACB = 1/2 ∠ AOB
Sudut keliling ACB = 1/2 . 98° = 49°.
Segitiga BOC adalah segitiga sama kaki karena panjang OB = OC = jari-jari lingkaran sehingga ∠ BCO = ∠ CBO = 21°.
Sudut ACO = 49° – 21° = 28°. Karena segitiga ACO sama kaki maka x = ∠ ACO = 28°.
Contoh soal 3

Pada gambar disamping ∠ DBC = 30° dan ∠ ADB = 27°. Tentukanlah:
- Sudut DAC
- Sudut ACB
Pembahasan
Jawaban soal 1: sudut DAC dan sudut DBC menghadap busur yang sama yaitu busur CD. Dengan demikian ∠DAC = ∠DBC = 30°.
Jawaban soal 2: sudut ACB dan sudut ADB menghadap busur yang sama yaitu busur AB. Sehingga ∠ACB = ∠ADB = 27°.
Contoh soal 4
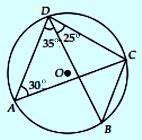
Pada gambar disamping ini sudut CAD = 30°, sudut ADB = 35° dan sudut ADC = 60°. Tentukan:
- Sudut CBD
- Sudut BCA
- Sudut ACD
Pembahasan
Jawaban soal 1: sudut CBD dan sudut CAD menghadap busur yang sama yaitu busur CD sehingga ∠CBD = ∠CAD = 30°.
Jawaban soal 2: sudut BCA dan sudut ADB menghadap busur yang sama yaitu busur AB sehingga ∠BCA = ∠ ADB = 35°.
Jawaban soal 3
Jumlah sudut segitiga ACD = 180°
∠CAD + ∠ADB + ∠BDC + ∠ACD = 180°.
30° + 35° + 25° + ∠ACD = 180°
90° + ∠ACD = 180°
∠ACD = 180° – 90° = 90°
Contoh soal 5
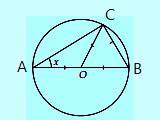
Hitunglah nilai x dari gambar disamping ini.
Pembahasan
Segitiga BOC adalah segitiga sama sisi sehingga ketiga sudutnya 60 sehingga BOC = 60. Karena sudut BOC dan sudut x menghadap busur yang sama yaitu busur CB maka x = 1/2 ∠BOC = 1/2 . 60° = 30°.
Cara lain menjawab soal ini sebagai berikut:
Sudut ACB adalah sudut yang menghadap diameter sehingga dipastikan siku-siku atau ∠ACB = 90°. Karena segitiga BCO sama kaki maka ketiga sudutnya = 60°. Jadi:
- ∠ACO = 90° – 60° = 30°
- ∠AOC = 180° – 60° = 120°
Jumlah sudut segitiga AOC = 180° atau:
- ∠CAO + ∠AOC + ∠ACO = 180°
- x + 120° + 30° = 180
- x + 150° = 180°
- x = 180° – 150° = 30°
Contoh soal 6

Perhatikan gambar disamping ini. Tentukanlah:
- Sudut OBC
- Sudut BAC
Pembahasan
Jawaban soal 1: segitiga BOC adalah segitiga samakaki sehingga ∠OBC = ∠OCB. Dengan menggunakan jumlah sudut segitiga = 180° diperoleh:
- ∠OBC + ∠OCB + ∠ BOC = 180°
- 2 ∠OBC + 88° = 180°
- 2∠OBC = 180° – 88° = 92°
- ∠OBC = 92°/2 = 46°
Jawaban soal 2: sudut BAC dan sudut pusat BOC menghadap busur yang sama yaitu busur BC sehingga sudut BAC = 1/2 . sudut BOC = 1/2 . 88° = 44°.
Contoh soal 7
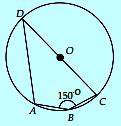
Gambar disamping ini adalah sebuah lingkaran dengan pusat O dan sudut ABC = 150°. Hitunglah sudut ADC.
pembahasan
∠ABC = 1/2 (sudut refleksi AOC)
150° = 1/2 (360° – ∠AOC)
300° = 360° – ∠AOC
∠AOC = 360° – 300° = 60°
Sudut ADC dan sudut pusat AOC menghadap busur yang sama yaitu busur AC sehingga sudut ADC = 1/2 . sudut AOC = 1/2 . 60° = 30°.