Postingan ini membahas contoh soal gerak pada bidang miring yang disertai pembahasannya atau penyelesaiannya. Gerak pada bidang miring merupakan salah satu penerapan hukum-hukum Newton tentang gerak.
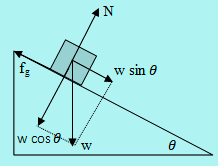
Gambar diatas menunjukkan gaya-gaya yang bekerja pada benda/balok yang diletakkan di bidang miring. Pada keadaan tersebut berlaku persamaan:
- w sin θ – fg = m . a.
- a = g sin θ (jika bidang miring licin)
Keterangan:
- w = berat benda (N)
- θ = sudut kemiringan
- fg = gaya gesekan (N)
- N = gaya normal (N)
Untuk lebih jelasnya perhatikan contoh soal dan pembahasannya dibawah ini.
Contoh soal 1
Sebuah balok dilepaskan dari bidang miring licin sempurna dengan sudut kemiringan 30° terhadap bidang datar. Jika g = 10 m/s2 maka percepatan yang dialami balok sebesar…
A. 20 m/s2
B. 15 m/s2
C. 10 m/s2
D. 5 m/s2
E. 2 m/s2
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- θ = 30°
- g = 10 m/s2
- fg = 0 (licin)
Maka percepatan balok dihitung dengan rumus sebagai berikut:
- a = g sin θ
- a = 10 m/s2 . sin 30° = 10 m/s2 . 1/2 = 5 m/s2
Jadi soal ini jawabannya D.
Contoh soal 2
Sebuah balok bermassa 5 kg dilepas dari bidang licin seperti gambar dibawah ini.

Jika g = 10 m/s2 dan tan 37° = 3/4 maka percepatan balok adalah…
A. 10 m/s2
B. 8 m/s2
C. 7,5 m/s2
D. 6 m/s2
E. 4,5 m/s2
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- m = 5 kg
- g = 10 m/s2
- tan θ = 3/4
- w = m . g = 5 kg . 10 m/s2 = 50 N
Selanjutnya kita menentukan nilai sin θ dengan cara sebagai berikut:

→ sin 37° =
→ Nilai C diperoleh dari C = √ 32 + 42 = 5
Percepatan balok dihitung dengan rumus sebagai berikut:
- a = g sin θ
- a = 10 m/s2 . 3/5 = 6 m/s2
Soal ini jawabannya D.
Contoh soal 3
Sebuah balok ditahan dipuncak bidang miring seperti gambar dibawah ini.
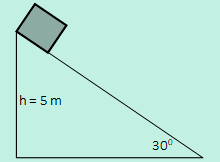
Ketika dilepas balok meluncur tanpa gesekan sepanjang bidang miring. Kecepatan balok ketika mencapai dasar bidang miring adalah…
A. 16 m/s
B. 12 m/s
C. 10 m/s
D. 8 m/s
E. 6 m/s
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- h = 5 m
- g = 10 m/s2
- θ = 30°
Cara menentukan kecepatan balok sebagai berikut:
→ a = g sin θ = 10 m/s2 sin 30° = 5 m/s2Menghitung panjang lintasan miring (s):
→ sin 30° =
→ s =
Menghitung kecepatan:
→ v = √ 2 . a . s = √ 2 . 5 . 10 = √ 100 = 10 m/s
Soal ini jawabannya C.
Contoh soal 4
Sebuah balok meluncur pada bidang miring licin seperti gambar dibawah ini.
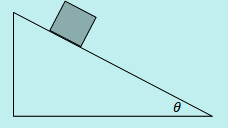
Jika g = 9,8 m/s2 dan tan θ = 3/4 maka jarak yang ditempuh balok selama 2 sekon adalah….
A. 11,76 m
B. 10,52 m
C. 9,8 m
D. 6,25 m
E. 5,88 m
Pembahasan / penyelesaian soal
Cara menjawab soal ini sebagai berikut:
→ tan θ = 3/4 maka sin θ = 3/5.→ a = g sin θ = 9,8 m/s2 . 3/5 = 5,88 m/s2
→ S = vo t + 1/2 . a . t2
→ S = 0 . 2 s + 1/2 . 5,88 m/s2 . (2 s)2 = 11,76 m
Soal ini jawabannya A.
Contoh soal 5
Perhatikan gambar dibawah ini.

Sebuah balok bermassa 8 kg mula-mula diam lalu ditarik dengan gaya F ke atas sejajar bidang miring. Jika koefisien gesekan 0,5 dan θ = 45° maka agar balok tepat akan bergerak keatas, gaya F harus = …
A. 80 √ 2 N
B. 80 N
C. 60 √ 2 N
D. 60 N
E. 40 N
Pembahasan / penyelesaian soal
Pada soal ini diketahui:
- m = 8 kg
- μ = 0,5
- θ = 45°
- a = 0 (tepat akan bergerak)
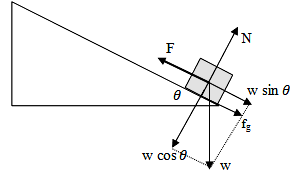
Berdasarkan gambar diatas kita peroleh hubungan sebagai berikut:
- F – w sin θ – fg = m . a
- F – 80 N sin 45° – μ . N = 8 kg . 0
- F – 80 N . 1/2 √ 2 – μ . w cos 45° = 0
- F = 40 √ 2 N + 0,5 . 80 N. 1/2 √ 2 = 0
- F = 40 √ 2 N + 20 √ 2 N = 60 √ 2 N
Soal ini jawabannya C.
Contoh soal 6
Perhatikan gambar dibawah ini.
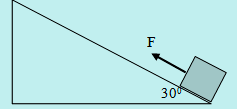
Sebuah balok berada pada bidang miring kasar ditarik dengan gaya F = 200 N. Jika massa balok 18 kg dan percepatan 3 m/s maka gaya gesekan yang dialami balok terhadap bidang miring sebesar…
A. 54 N
B. 56 N
C. 90 N
D. 126 N
E. 180 N
Pembahasan / penyelesaian soal
Cara menjawab soal ini sebagai berikut:
- F – w sin θ – fg = m . a
- fg = F – w sin θ – m . a
- fg = 200 N – 18 kg . 10 m/s2 . sin 30° – 18 kg . 3 m/s2
- fg = 200 N – 90 N – 54 N = 56 N
Soal ini jawabannya B.