Postingan ini membahas contoh soal determinan matriks, transpose matriks dan pembahasannya atau penyelesaiannya. Determinan matriks ditulis dengan det (A) atau |A|. Transpose matriks A, ditulis At adalah matriks yang elemen-elemennya diperoleh dari elemen-elemen matriks A dengan mengubah setiap elemen baris ke-n dari matriks A menjadi elemen kolom ke-n dari matrik At dan setiap elemen kolom ke-m matriks A menjadi elemen baris ke-m dari matriks At.
Cara menentukan determinan matriks ordo 2 x 2, misalkan matriks maka determinan A = det (A) = a . d – b . c.
Jika matriks A berordo 3 x 3 maka cara menentukan determinannya seperti gambar dibawah ini:

Jadi determinan matriks A = det (A) = (a . e . i) + (b . f . g) + (c . d . h) – (c . e . g) – (a . f . h) – (b . d . i).
Transpose matriks adalah mengubah baris menjadi kolom atau sebaliknya. Cara menentukan transpose matriks sebagai berikut:
Contoh soal determinan matriks
Contoh soal 1
Tentukan determinan dari matriks .
Pembahasan / penyelesaian soal
Pada matriks A kita ketahui a = 3, b = 4, c = 5 dan d = 6. Jadi determinan A = det (A) = a.d – b.c = 3 . 6 – 4 .5 = 18 – 20 = -2.
Contoh soal 2
Hitunglah determinan matriks .
Pembahasan / penyelesaian soal
Untuk menentukan determinan matriks B dengan cara seperti gambar dibawah ini:

Jadi determinan matriks B = det (B) = (1 . 3 . 2) + (3 . -1. 4) + (1 . 2 . 0) – (1 . 2 . 4) – (1 . -1 . 0) – (3 . 2 . 3) = 6 + (-12) + 0 – 8 – 0 – 18 = -32.
Contoh soal 3
Hitunglah determinan matriks berordo 3 x 3 .
Pembahasan / penyelesaian soal
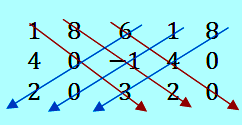
Det (C) = (1 . 0 . 3) + (8 . -1 . 2) + (6 . 4 . 0) – (6 . 0 . 2) – (1 . -1 . 0) – (8 . 4 . 3) = 0 + (-16) + 0 – 0 – 0 – 96 = – 112.
Contoh soal 4 (UN 2017 IPS)
Diketahui matriks dan
. Determinan A x B adalah…
A. -391
B. -119
C. -41
D. 41
E. 291
Pembahasan \ penyelesaian soal
Untuk menjawab soal ini, hitung terlebih dahulu hasil dari A x B sebagai berikut:
Dari hasil tersebut diketahui a = -5, b = 9, c = 24 dan d = 35 sehingga determinan matriks AB = a.d – b.c = -5 . 35 – 9 . 24 = -175 – 216 = -391. Jadi soal ini jawabannya adalah A.
Contoh soal 5 (UN 2015 IPA)
Diketahui matriks dan
. Determinan matriks PQ adalah…
A. 225
B. 156
C. 81
D. 11
E. 9
Pembahasan / penyelesaian soal
Sama seperti nomor 4 kita hitung terlebih dahulu matriks PQ yaitu:
Berdasarkan matriks PQ kita ketahui a = 27, b = -3, c = 39 dan d = -4 sehingga determinan PQ = a.d – b.c = 27 . -4 – (-3) . 39 = -108 + 117 = 9. Jadi soal nomor 2 jawabannya adalah E.
Contoh soal 6 (UN 2014 IPS)
Diketahui matriks ,
dan
. Determinan matriks (P + Q – 2R) adalah ….
A. 32
B. -12
C. 12
D. 20
E. 52
Pembahasan / penyelesaian soal
Hitung terlebih dahulu matriks P + Q yaitu:
Selanjutnya hitung 2R sebagai berikut:
Kemudian kita hitung (P + Q) – 2R):
Berdasarkan hasil diatas kita peroleh a = 4, b = 5, c = -4 dan d = -8. Jadi determinan P + Q – 2R = a.d – b.c = 4 . (-8) – 5 . (-4) = -32 + 20 = -12. Jawaban soal nomor 3 adalah B.
Contoh soal transpose matriks
Contoh soal 1
Tentukan transpose matriks .
Pembahasan / penyelesaian soal
Contoh soal 2
Tentukan transpose matriks dari .
Pembahasan / penyelesaian soal
Contoh soal 3
Tentukan transpose matriks dari .
Pembahasan / penyelesaian soal
Contoh soal 4 (UN 2019 IPA)
Diketahui matriks ,
dan
. Jika A – B = CT, nilai x + y adalah…
A. 3
B. 5
C. 7
D. 8
E. 9
Pembahasan / penyelesaian soal
Untuk menjawab soal ini hitung terlebih dahulu A – B:
Selanjutnya kita tentukan transpose matriks C sebagai berikut:
Jadi A – B = CT sebagai berikut:
Berdasarkan hubungan diatas kita peroleh:
- 3 – x = 4 maka x = 3 – 4 = – 1
- y – 10 = -1 maka y = -1 + 10 = 9
Jadi x + y = -1 + 9 = 8. Jawaban soal nomor 1 adalah D.
Contoh soal 5 (UN 2018 IPS)
Diketahui matriks ,
,
dan
. Jika 2A + BT = CD dan BT = transpose B, nilai a + b – c adalah…
A. -8
B. -6
C. -4
D. 6
E. 8
Pembahasan / penyelesaian soal
Tentukan terlebih dahulu transpose matriks B yaitu:
Selanjutnya kita tentukan hasil 2A + BT yaitu:
Kemudian kita tentukan matriks CD sebagai berikut:
Jadi kita peroleh hubungan A + BT = CD sebagai berikut:
Sehingga kita peroleh:
- 2a + 6 = 2 atau 2a = 2 – 6 = -4 maka a = -2
- 2b – 8 = -6 atau 2b = -6 + 8 = 2 atau b = 1
- 9 = -1 + 2c atau 2c = 9 + 1 = 10 maka c = 5
Jadi hasil dari a + b – c = -2 + 1 – 5 = -6. Jawaban soal nomor 2 adalah B.
Contoh soal 6 (UN 2018 IPS)
Diketahui matriks ,
,
dan
. Jika 3A + BC = DT ; (DT = transpose D, nilai dari 2x + 3y -z adalah…
A. -18
B. -14
C. -12
D. -8
E. 14
Pembahasan / penyelesaian soal
Hitung hasil dari BC:
Kemudian hitung 3A + BC:
Transpose matriks D:
Jadi diperoleh hubungan 3A + BC = DT:
Dari hubungan tersebut kita peroleh:
- 3x – 4 = -7 maka x = -1
- z = 3
- 9 – y = 8 atau y = 1
Jadi 2x + 3y – z = 2 . (-1) + 3 (1) – 13 = -2 + 3 – 13 = -12. Jawaban C.