Lompat ke konten

7 Contoh soal peluang majemuk dan pembahasannya

Contoh soal peluang majemuk nomor 1

Diketahui kejadian A dan kejadian B dengan P(A) = 1/2, P(B) = 1/3, dan P (A ∩ B) = 1/4, maka P(A ∪ B) = …
A. 7/12
B. 2/3
C. 3/4
D. 7/8
E. 11/12

Pembahasan

  • P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
  • P (A ∪ B) = \frac {1} {2} + \frac {1} {3} – \frac {1} {4}
  • P (A ∪ B) = \frac {5} {6} – \frac {1} {4} = \frac {10 - 3} {12} = \frac {7} {12}

Soal ini jawabannya A.

Contoh soal peluang majemuk nomor 2

Sebuah kartu diambil secara acak dari satu set kartu bridge. Peluang terambil kartu merah atau kartu As adalah …
A. \frac {24} {52}
B. \frac {26} {52}
C. \frac {28} {52}
D. \frac {30} {52}
E. \frac {32} {52}

Pembahasan

Yang termasuk kartu merah adalah kartu wajik dan kartu hati, dengan jumlah = 26. Kartu As dengan jumlah = 4.

Diketahui:

  • peluang terambil kartu merah = P(A) = \frac {26} {52}
  • Peluang terambil kartu As = P(B) = \frac {4} {52}
  • Peluang terambil kartu merah dan kartu As = P (A ∩ B) = \frac {2} {52}

Maka peluang terambil kartu merah atau kartu As sebagai berikut.

  • P (A ∪ B) = P(A) + P(B) – P (A ∩ B)
  • P (A ∪ B) = \frac {26} {52} + \frac {4} {52} – \frac {2} {52}
  • P (A ∪ B) = \frac {30} {52} – \frac {2} {52} = \frac {30 - 2} {52} = \frac {28} {52}

Soal ini jawabannya C.

Contoh soal peluang majemuk nomor 3

Pada pelemparan dua dadu satu kali, peluang munculnya mata dadu berjumlah 8 atau 5 adalah …
A. 5/19
B. 1/4
C. 5/26
D. 1/9
E. 2/9

Pembahasan

Mata dua dadu

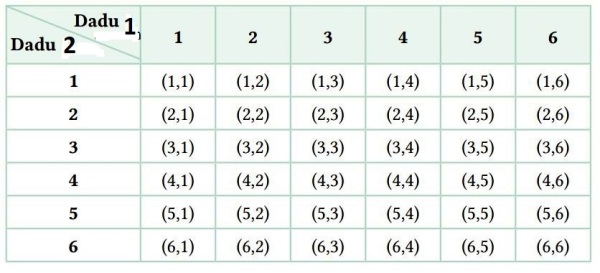
Mata dadu berjumlah 8 (A) = (2, 6) ; (3, 5) ; (4, 4) ; (5, 3) ; (6, 2). Jumlah n(A) = 5.
Mata dadu berjumlah 5 (B) = (1, 4) ; (2, 3) ; (3, 2) ; (4, 1). Jumlah n(B) = 4.

Maka peluang muncul mata dadu berjumlah 8 atau 5 sebagai berikut.

  • P (A ∪ B) = P(A) + P(B)
  • P (A ∪ B) = \frac {5} {36} + \frac {4} {36}
  • P (A ∪ B) = \frac {5 + 4} {36} = \frac {9} {36} = \frac {1} {4}

Soal ini jawabannya B.

Contoh soal peluang majemuk nomor 4

Dua dadu dilempar bersama-sama. Peluang munculnya jumlah mata dadu 9 atau 10 adalah …
A. 5/36
B. 7/36
C. 8/36
D. 9/36
E. 11/36

Pembahasan

  • Mata dadu berjumlah 9 (A) = (3, 6) ; (4, 5) ; (5, 4) ; (6, 3). Jumlah n(A) = 4.
  • Mata dadu berjumlah 10 (B) = (4, 6) ; (5, 5) ; (6, 4). Jumlah n(B) = 3.

Maka peluang muncul mata dadu 9 atau 10 sebagai berikut.

  • P (A ∪ B) = P(A) + P(B)
  • P (A ∪ B) = \frac {4} {36} + \frac {3} {36}
  • P (A ∪ B) = \frac {4 + 3} {36} = \frac {7} {36}

Soal ini jawabannya B.

Contoh soal peluang majemuk nomor 5

Dua dadu dilempar bersama-sama. Peluang muncul mata dadu pertama 3 dan mata dadu kedua 5 adalah ….
A. 6/36
B. 5/36
C. 4/36
D. 3/36
E. 1/36

Pembahasan

  • P (A ∩ B) = P(A) x P(B)
  • P (A ∩ B) = \frac {1} {6} x \frac {1} {6}
  • P (A ∩ B) = \frac {1} {36}

Soal ini jawabannya E.

Contoh soal peluang majemuk nomor 6

Sebuah kantong berisi 6 bola merah, 4 bola putih, dan 8 bola biru. Apabila 3 bola diambil sekaligus secara acak, peluang terambil 2 bola putih dan 1 bola merah adalah …
A. 55/204
B. 5/204
C. 7/102
D. 3/68
E. 6/17

Pembahasan

Banyak cara mengambil 2 bola putih dari 4 bola putih:
→ 4C2 =
4!
2! . (4 – 2)!
 =
4 x 3 x 2!
2 x 1 x 2!
 = 6
Banyak cara mengambil 1 bola merah dari 6 bola merah:
→ 6C1 =
6!
1! . (6 – 1)!
 =
6 x 5!
1 x 5!
 = 6
Banyak cara mengambil 3 bola dari 18 bola:
→ n(S) = 18C3 =
18!
3! . (18 – 3)!
 =
18 x 17 x 16 x 15!
3 x 2 x 1 x 15!
 = 816
Jadi peluang terambil 2 bola putih dan 1 bola merah:
→ P(A ∩ B) =
6 x 6
816
 =
36
816
 = =
3
68

Soal ini jawabannya D.

Contoh soal peluang majemuk nomor 7

Sebuah kotak berisi 5 balon hijau dan 3 balon kuning. Dari kotak itu diambil 2 balon secara berurutan tanpa dikembalikan. Peluang kejadian terambil balon hijau pada pengambilan pertama dan balon kuning pada pengambilan kedua adalah …
A. 15/56
B. 18/56
C. 20/56
D. 25/56
E. 35/56

Pembahasan

  • P (A ∩ B) = P(A) x P(B)
  • P (A ∩ B) = \frac {3} {8} x \frac {5} {7}
  • P (A ∩ B) = \frac {15} {56}

Soal ini jawabannya A.

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *