8 Contoh soal luas daerah yang dibatasi kurva & pembahasan

Contoh soal luas daerah nomor 1

Luas daerah yang dibatasi oleh kurva y = x³ – 6x² + 8x dan sumbu X adalah …
A. 4
B. 6
C. 8
D. 10
E. 12

Pembahasan

• x³ – 6x² + 8x = 0
• x (x² – 6x + 8) = 0
• x (x – 4) (x – 2) = 0
• x = 0 dan x = 4 dan x = 2

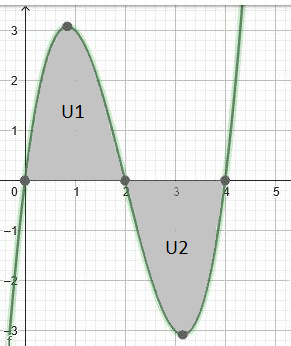
Luas daerah = U1 + U2
= [latex]\int_{0}^{2} (x^{3} – 6x^{2} + 8x) dx[/latex] + (- [latex]\int_{2}^{4} (x^{3} – 6x^{2} + 8x) dx[/latex]
= [latex]\left [ \frac {1} {4} x^{4} – 2x^{3} + 4x^2 \right ]_{0}^{2}[/latex] – [latex]\left [ \frac {1} {4} x^{4} – 2x^{3} + 4x^2 \right ]_{2}^{4}[/latex]
= (1/4 . 2⁴ – 2 . 2³ + 4 . 2²) – ((1/4 . 4⁴ – 2 . 4³ + 4 . 4²) – 1/4 . 2⁴ – 2 . 2³ + 4 . 2²))
= ((4 – 16 + 16) – 0) – ((64 – 128 + 64) – (4 – 16 + 16))
= 4 – (-4) = 4 + 4 = 8

Soal ini jawabannya C.

---

Contoh soal luas daerah nomor 2

Luas daerah yang dibatasi oleh kurva y = 2 – x² dan y = – x adalah …
A. 9/2
B. 7/2
C. 3
D. 5/2
E. 3/2

Pembahasan

• -x = 2 – x²
• x² – x – 2 = 0
• (x – 2) (x + 1) = 0
• x = 2 dan x = -1

Jadi luas daerah sebagai berikut.

= – [latex]\int_{-1}^{2} (x^{2} – x – 2) dx[/latex]
= – ([latex]\left [\frac {1} {3} x^{3} – \frac {1} {2} x^{2} – 2x \right ]_{-1}^{2}[/latex])
= – (1/3 . 2³ – 1/2 . 2² – 2 . 2) – (1/3 . (-1)³ – 1/2 . (-1)² – 2 . -1)
= – (8/3 – 2 – 4) – (- 1/3 – 1/2) + 2)
= – (8/3 – 18/3) – ((-2 – 3 + 12)/6))
= – (- 10/3 – 7/6)
= (20 + 7)/6 = 27/6 = 9/2.

Soal ini jawabannya A.

---

Contoh soal luas daerah nomor 3

Luas daerah yang dibatasi oleh kurva y = -x² + 2x, sumbu X, dan garis X = 3 adalah …
A. 0
B. 1 1/3
C. 2 2/3
D. 8
E. 4

Pembahasan

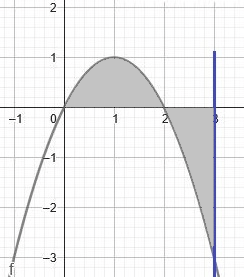
Luas daerah sebagai berikut.

= [latex]\int_{0}^{2} (-x^{2} + 2x) dx[/latex] + (- [latex]\int_{2}^{3} (-x^{2} + 2x) dx[/latex])
= ([latex]\left [- \frac {1} {3} x^{3} + x^2 \right ]_{0}^{2}[/latex]) – ([latex]\left [- \frac {1} {3} x^{3} + x^2 \right ]_{2}^{3}[/latex])
= ((- 1/3 . 2³ + 2²) – 0)) – ((- 1/3 . 3³ + 3²) – (- 1/3 . 2³ + 2²))
= (- 8/3 + 4) – ((-9 + 9) – (- 8/3 + 4))
= (- 8/3 + 4) + (- 8/3 + 4)
= -2 (8/3) + 4 + 4 = 8 – 16/3
= 24/3 – 16/3 = 8/3.

Jawaban: –

---

Contoh soal luas daerah nomor 4

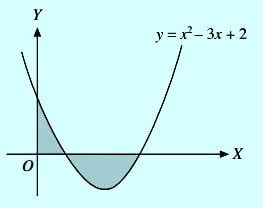
Luas daerah yang diarsir pada gambar di bawah adalah …
A. 1/6
B. 5/6
C. 2/3
D. 3/2
E. 1

Pembahasan

• x² – 3x + 2 = 0
• (x – 2) (x – 1) = 0
• x = 2 dan x = 1

Jadi luas daerah yang diarsir sebagai berikut

= [latex]\int_{0}^{1} (x^{2} – 3x + 2) dx[/latex] + (- [latex]\int_{1}^{2} (x^{2} – 3x + 2) dx[/latex])
= ([latex]\left [\frac {1} {3} x^{3} – \frac {3} {2} x^{2} + 2x \right ]_{0}^{1}[/latex]) – ([latex]\left [x^{3} – \frac {3} {2} x^{2} + 2x \right ]_{1}^{2}[/latex])
= ((1/3 . 1³ – 3/2 . 1² + 2 . 1) – 0) – ((1/3 . 2³ – 3/2 . 2² + 2 . 2) – (1/3 . 1³ – 3/2 . 1² + 2 . 1))
= (1/3 – 3/2 + 2) – ((8/3 – 6 + 4) – (1/3 – 3/2 + 2))
= (- 7/6 + 2) – ([8/3 – 2) – (- 7/6 + 2))
= (5/6) – (2/3 – 5/6)
= 5/6 +1/6 = 6/6 = 1

Soal ini jawabannya E.

---

Contoh soal luas daerah nomor 5

Luas daerah yang dibatasi kurva y = x² dan y = x + 2 adalah …
A. 9
B. 27/8
C. 27/6
D. 9/6
E. 9/7

Pembahasan

• x² = x + 2
• x² – x – 2 = 0
• (x – 2) (x + 1) = 0
• x = 2 dan x = -1

Luas daerah sebagai berikut.

= – [latex]\int_{-1}^{2} (x^{2} – x – 2) dx[/latex]
= – ([latex]\left [\frac {1} {3} x^{3} – \frac {1} {2} x^{2} – 2x \right ]_{-1}^{2}[/latex])
= – (1/3 . 2³ -1/2 . 2² – 2 . 2) – (1/3 . (-1)³ – 1/2 . (-1)² – 2 . -1)
= – (8/3 – 2 – 4) – (- 1/3 – 1/2) + 2)
= – (8/3 – 18/3) – (-2 – 3 + 12)/6))
= – (- 10/3 – 7/6)
= (20 + 7)/6 = 27/6.

Soal ini jawabannya C.

---

Contoh soal luas daerah nomor 6

Luas daerah yang dibatasi kurva y = 4x dan y = 3 dari x = 1 sampai x = 2 adalah … satuan luas.
A. 1
B. 2
C. 3
D. 5
E. 6 2/3

Pembahasan

Luas daerah yang diarsir sebagai berikut.

= [latex]\int_{1}^{2} (4x – 3) dx[/latex]
= [latex]\left [2x^{2} – 3x \right ]_{1}^{2}[/latex]
= (2 . 2² – 3 . 2) – (2 . 1² – 3 . 1)
= (8 – 6) – (-1) = 2 + 1 = 3

Soal ini jawabannya C.

---

Contoh soal luas daerah nomor 7

Luas bidang yang dibatasi oleh grafik y = 6x² – x dan sumbu-x adalah …
A. 1/36 satuan luas
B. 1/72 satuan luas
C. 1/108 satuan luas
D. 1/216 satuan luas
E. 1/432 satuan luas

Pembahasan

• 6x² – x = 0
• 6x (x – 1) = 0
• x = 0 dan x = 1

Luas daerah sebagai berikut.

= [latex]\int_{0}^{1} (6x^{2} – x) dx[/latex]
= [latex]\left [2x^{3} – \frac {1} {2} x^{2} \right ]_{0}^{1}[/latex]
= (2 . 1³ – 1/2 . 1²) – (0)
= 2 – 1/2 = 3/2

Jawaban: –

---

Contoh soal luas daerah nomor 8

Luas daerah terbatas di bawah ini adalah …
A. 4/3
B. 10/3
C. 8/3
D. 2
E. 1

Pembahasan

= [latex]\int_{-1}^{1} (-x^{2} + 1) dx[/latex] + (- [latex]\int_{1}^{2} (-x^{2} + 1) dx[/latex])
= [latex]\left [- \frac {1} {3} x^{3} + x \right ]_{-1}^{1}[/latex] – ([latex]\left [- \frac {1} {3} x^{3} + x \right ]_{1}^{2}[/latex])
= (((- 1/3 . (1)³ + (1)) – (- 1/3 . (-1)³ + (-1))) – (((- 1/3 . (2)³ + 2) – (- 1/3 . (1)³ + (1)))
= (- 1/3 + 1 + 2/3) – ((- 8/3 + 2) – 2/3)
= 4/3 + 4/3 = 8/3

Soal ini jawabannya C.